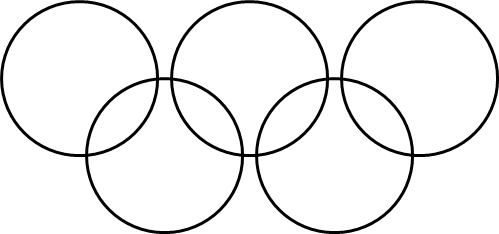
図のように色がぬられていない5つの輪が並んでいます。この輪の線に色をぬるとき、次の問いに答えなさい。ただし,線が重なる輪には同じ色をぬれないものとします。
(1) 青,黄,黒,緑,赤の5色をすべて使って色をぬる方法は何通りありますか。
(2) 青,黄,緑,赤の4色をすべて使って色をぬる方法は何通りありますか。
(3) 緑は青と黄を混ぜた色と考えて,緑と青,緑と黄は線が重なる輪には色をぬれないものとします。このとき,青,黄,黒,緑,赤の5色をすべて使って色をぬる方法は何通りありますか。
栄東中学・A日程(2020年)
1月受験の代表校である栄東中学より「場合の数」の問題です。以下の過去問解説記事の使い方を読み、得点力アップや弱点補強にご活用ください。
本問題の難度
Lv.3 中学受験 難関校標準問題
中学受験 難関校の標準問題。難関校合格のために必要な標準問題を確実に正答する力をつけたい受験生や、合否を分ける問題を1問でも多く正答できるように得点力をアップさせたい中堅校志望の受験生にオススメ。
※偏差値の目安やその他難度の詳細などはコチラをご覧ください。
解説
(1) 青,黄,黒,緑,赤の5色をすべて使って色をぬる方法
 プロ家庭教師K
プロ家庭教師K場合の数の色ぬり問題ですね。ステップ通り、解き進めていきましょう。
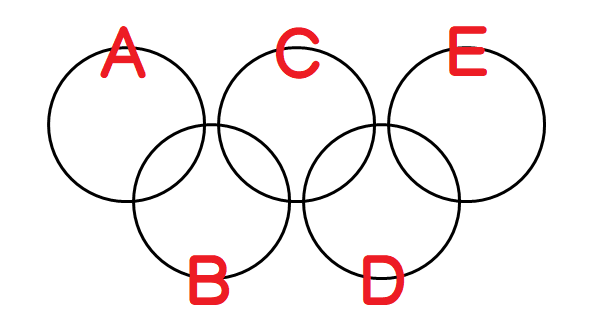
色をぬる部分に名前を付けます。A,Bやア,イなど書きやすくシンプルな名前にしておきましょう。
STEP1で分けた、ブロックのどこが同じ色になるか、違う色になるか、ぬり方のパターンを考えます。
(1)は5つの輪を5色すべてを使ってぬる必要がありますので、A,B,C,D,Eすべて違う色となり、ぬり方は1パターンとなります。
色の入れ方です。この最後のSTEP3でいよいよ赤,青など具体的な色名が出てきます。STEP3では、「〇ヵ所を〇色でぬるか」を考えて、通り数を出します。
(1)は5ヵ所を5色すべて使ってぬるので、5×4×3×2×1=120通りとなります。
(2) 青,黄,緑,赤の4色をすべて使って色をぬる方法

ぬり方のパターンは?
(2)は、5つの輪を4色すべてを使ってぬり分けるので、どこか2ヵ所は同じ色となります。ぬり方のパターンは以下の通り、6パターンあります。
- A=C,B,D,E (AとCが同じ色で、B,D,Eは他の3色という意味)
- A=D,B,C,E
- A=E,B,C,D
- B=D,A,C,E
- B=E,A,C,D
- C=E,A,B,D
色のいれ方は?
次に、色のいれ方です。何か所を何色でぬるか?ですが、同じ色の部分は1ヵ所と考えます。よって、6パターン全て「4ヵ所を4色で入れる」なので、4×3×2×1=24通り。
6×24=144通りが答えとなります。
(3) 緑と青,緑と黄は重なってはいけないものとしたとき,青,黄,黒,緑,赤の5色をすべて使って色をぬる方法

緑が青・黄と重なってはいけないという新たなルールが加わりました。1番制限の多い「緑」の位置を決めて、場合分けして考えてみましょう。
緑がAの場合
緑がAの場合は、Aと重なっているBに「青」「黄」を入れてはいけません。つまり、Bに入る色は「黒」か「赤」の2通りとなります。残りのC,D,EはAと重ならない部分ですので、特に制限はありません。Cに入る色は残り3色、Dに入る色は残り2色、…と考えて、C,D,Eの色のいれ方は3×2×1=6通り。
よって、緑がAの場合は2×6=12通りです。
緑がBの場合
緑がBの場合は、Bと重なっているAとCに「青」「黄」を入れてはいけません。つまり、AとCに入る色は「黒」か「赤」となり、その通り数は2×1=2通りです。残りのDとEはBと重ならない部分ですので、特に制限はありません。D,Eの色の入れ方は2×1=2通りです。
よって、緑がBの場合は2×2=4通りです。
緑がCの場合
緑がCの場合は、Cと重なっているBとDに「青」「黄」を入れてはいけません。つまり、BとDに入る色は「黒」か「赤」となり、その通り数は2×1=2通りです。残りのAとEはCと重ならない部分ですので、特に制限はありません。A,Eの色の入れ方は2×1=2通りです。
よって、緑がCの場合は2×2=4通りです。
緑がDの場合
五輪の輪は左右対称な図形です。条件が同じ場合は、通り数も同じになりますので、活用しましょう。
よって、緑がDの場合は、緑がBの場合と同じ4通りです。
緑がEの場合
緑がEの場合は、緑がAの場合と同じ12通りです。
よって、場合分けした結果を全て足し、12+4+4+4+12=36通りが答えになります。
Kとピヨまるの談話室
 ピヨまる
ピヨまる東京五輪も紆余曲折を乗り越え、開幕となりましたね。
この談話室でも「算数も時事問題がある!」という話がたまに出てきますが、今回の問題はオリンピック関連でしょうか。
 プロ家庭教師K
プロ家庭教師Kそうだね。オリンピック関連だと今回のように五輪の輪を使ったものや、他にもトーナメント戦、総当たり戦などの試合と絡めた問題、得点や順位に着目した推理と論証のような問題も考えられるかな。
ただ、社会の時事問題のように何か特定の単語を知らないと解けないとかはないよ。
こちらの記事もオススメ☆
・栄東中学の算数分析/過去問解説はコチラ
・過去問解説記事の一覧はコチラ
・場合の数の過去問解説はコチラ
・その他の難関校標準問題(★★★☆☆)はコチラ