速さ / 時計算（巣鴨中学 2017年）

時計の長針と短針の位置関係について、次の各問いに答えなさい。ただし、答えが割り切れないときは、分数で答えなさい。

（１）０時30分のとき、長針と短針の作る角のうち小さい方の角度を求めなさい。
（２）０時からスタートして、最初に長針と短針が一直線になる時刻は何時何分ですか。
（３）８時から９時の間で、時計の長針と短針の位置が６のめもりをはさんで左右対称となる時刻は何時何分ですか。

巣鴨中学（2017年）

2020年入試にて倍率がグンと上がった巣鴨中学。そんな人気男子校より時計算の問題の紹介です。(１)(２)は時計算の基本問題なので、確実に取りましょう。(３)も時計算を学ぶ際に必ず触れる標準問題ですので、確認の意味も込めて是非トライしてみてください♪

解説

（１）０時30分のとき、長針・短針の間の角は？

時計算ではまず基準となる時間を考えましょう。０時30分を考えるとき、基準となる時間は０時00分です。０時00分のときの長針・短針は重なっているので、間の角は０°ですね。

０時00分からは長針と短針はどんどん離れていきます。長針は１分で６°、短針は１分で0.5°動くので、長針と短針は１分で5.5°離れることが分かります。

よって、０時30分のときは5.5°×30分＝165°
今回は「長針と短針の作る角のうち小さい方の角度」を聞かれていますので、解答用紙に記入する答えが180°以下になっているかも必ずチェックしましょう。

A.165°

（２）０時～１時の間で長針・短針が最初に一直線になるのは？

０時～１時の間ですので、基準となる時間は（１）と同様に０時00分となります。
０時00分のときの長針・短針は重なっているので、間の角は０°です。

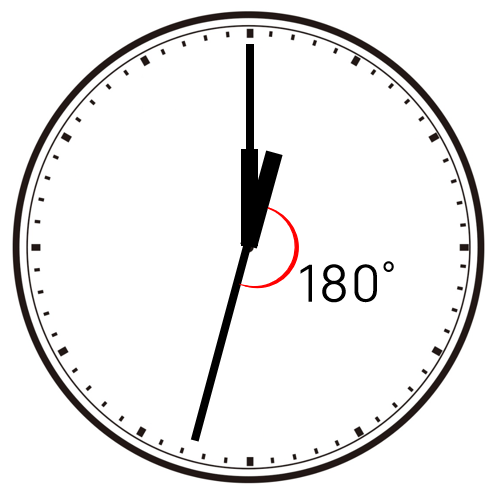
長針・短針が一直線になるのは間の角が180°となったときなので、０°の状態から180°離れたときの時間が答えとなります。
長針と短針は１分で5.5°離れていくので、180°×\(\large{\frac{2}{11}}\) = 32\(\large{\frac{8}{11}}\)分のときに長針・短針が一直線になる。

A.０時32\(\large{\frac{8}{11}}\)分

（３）８時～９時の間で時計の長針・短針が６の目盛りを境に左右対称になるには？

こちらもまずは基準となる時間を描きましょう。基準となる時間は８時00分です。
次に、８時～９時の間で長針・短針が６の目盛りを境に左右対称になる時をイメージして、長針・短針を描きましょう。

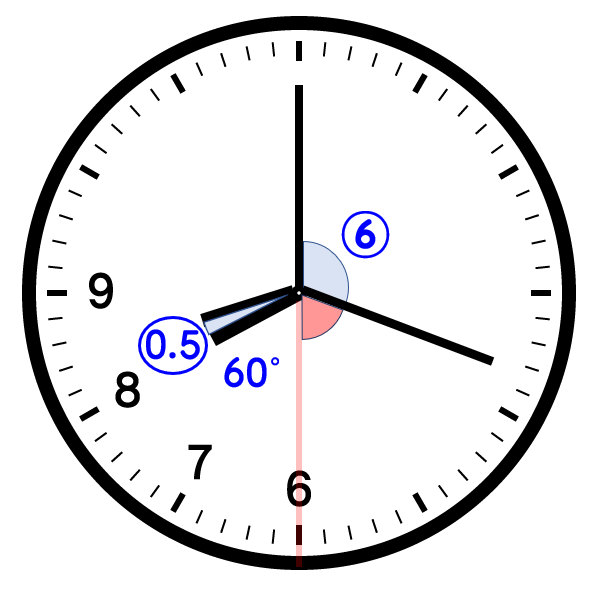
長針は１分６°、短針は１分0.5°、対象の軸である６時と８時との間の角は60°。
長針・短針が６の目盛りを境に線対称であることを利用すると、それぞれの角を以下のように表すことが出来ます。

よって、120÷6.5＝18\(\large{\frac{6}{13}}\)分のときに長針・短針は６の目盛りを境に左右対称となる。

A.8時18\(\large{\frac{6}{13}}\)分

対面型の家庭教師とオンライン指導の２つのサービスを提供しています。
オンライン指導は１回20分～のスポット指導も可能。指導依頼は上記バナーをクリックし、料金・条件等をご確認の上、お申し込みください！

「全308問徹底添削の算数基礎講座」や「オリジナル算数教材」を販売しています。是非ご覧ください！