芝中学の算数分析と対策（2017年第1回）

男子難関校の芝中学の算数分析記事です。今回の過去問分析対象は「2017年第1回入試」となります。芝中学算数の問題構成や傾向、難易度を知り、合格に向けた志望校対策につなげてください。

芝中学 2017年入試結果

配点・試験時間

• 国語　100点（50分）
• 算数　100点（50分）
• 社会　75点（40分）
• 理科　75点（40分）

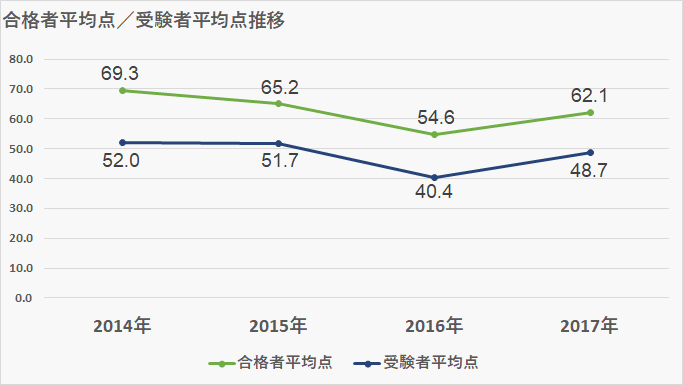
合格者平均点・受験者平均点

• 合格者平均点－62.1点
• 受験者平均点－48.7点

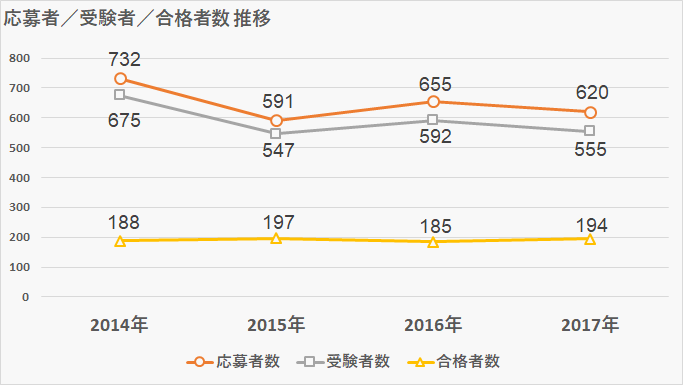
受験者数・合格者数

• 募集者数：150人
• 応募者数：620人
• 受験者数：555人
• 合格者数：194人
  

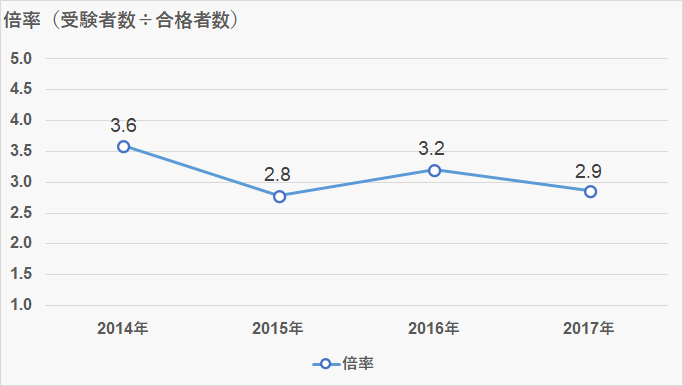
実質倍率

• 倍率：2.9倍

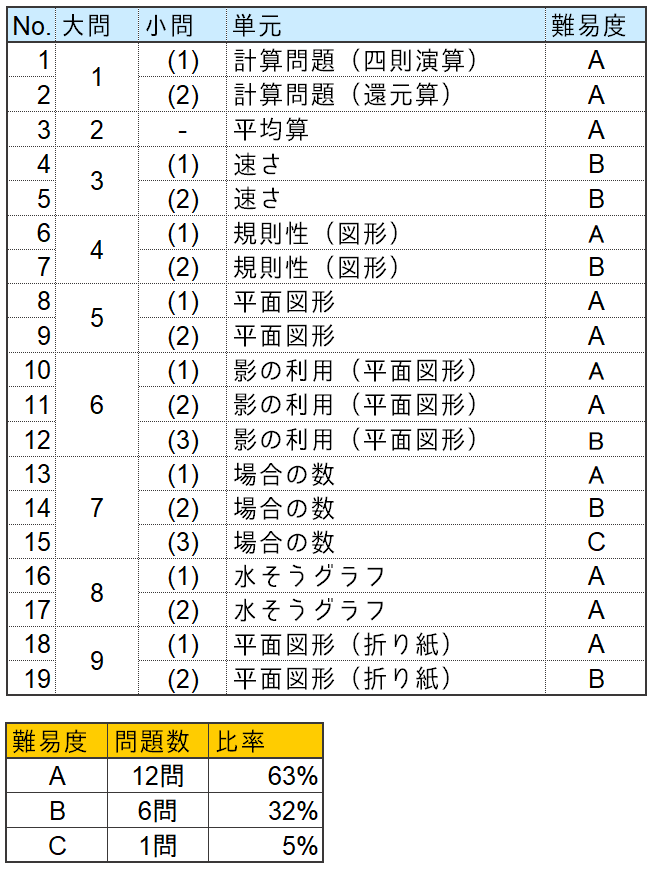
問題別難易度分析

【難易度説明】
A：芝中学合格のために正答したい問題
B：合否を分ける差がつく問題
C：発展問題（間違えても差がつかない）

問題別攻略のポイント

大問１　計算問題

問題数：２
難易度：A，A

(１)　四則演算

例年出題されている標準的な計算問題です。0.75×1.6を小数のまま計算するのか、分数に変えて計算するのか、はたまた小数、分数をミックスして計算するのかなどの判断を素早く行いましょう。また、0.75や1.6は一発で仮分数に変形できているか確認しておきましょう。

(２)　還元算

こちらも標準的な計算問題です。＋－×÷や()など計算ルールに則り、逆算して答えを出します。芝中学の計算問題は答えを出すまでのステップがそれなりに多いので、計算する順序が間違えていないか、今何の計算をしているのかを常に考えながら、ていねいに進めていきましょう。
計算問題も試験の最後にある難問も、１問の配点はほとんど変わりありません。合格をつかみ取るために、計算問題でしっかりと点を取っておくことが重要であることを理解しておいてください。

大問２　平均算

問題数：１
難易度：A

基本的な平均算です。平均点72点を基準に、合格者の集団と不合格者の集団を面積図で表し、解きましょう。

大問３　速さ（坂道問題）

問題数：２
難易度：B，B

速さの坂道問題です。難易度だけ考えればAでも良かったですが、差がつきやすい問題なのでBにしています。
このような坂道問題は、上りと下りの差に着目しましょう。例えば、Ａ～BまでとB～Cまでの距離が同じであれば、行き帰りの上り、下りの距離は同じですので、行き帰りの時間に差は生まれません。つまり、行き帰りの時間に10分の差が生まれているのは、A～BまでとB～Cまでの距離の差である５kmの部分が原因であることが分かります。
そこから、攻めていきましょう。

(１)が解けていれば、あとは難しくないでしょう。上り、下りそれぞれの速さ、時間、距離を使い、A～B間にかかる時間を考えましょう。

大問４　規則性（図形）

問題数：２
難易度：A，B

規則性は何と何の関係性を聞かれているか？に着目する事が非常に重要です。

(１)は、●印が108個あるときの図形のまわりの長さを聞かれているので、●印の個数と図形のまわりの長さの関係性を聞かれています。問題文に書かれている３つを使って、上記の関係性を考えましょう。

(２)は、図形の面積と●印の個数の関係性を聞かれています。図形の面積は2cm×2cmの面がいくつあるかで決まるので、面の数と●印の個数の関係性を考えてみましょう。

大問５　平面図形

問題数：２
難易度：A，A

(１)は、△AEHと△GDHの相似を利用し、△AEHの面積を出しましょう。高さが等しいとき、底辺の長さの比は面積比と等しいという基本ポイントを使います。

(２)は、□EFGHの面積を出すので、□EBGDから△GDHと△BEFの面積を引いて求めましょう（□AECGを使ってもよい）。パッと見で□EBGDを平行四辺形と勘違いし、□EFGHの面積を誤ってしまった子もいるのではないでしょうか？
図形問題では図を見た目通りに信じてはいけません。辺の長さも角度もしっかりと実際の数値を確認して解きましょう。

大問６　影の利用（平面図形）

問題数：３
難易度：A，A，B

(１)は、光がまっすぐ進む性質を使った影の問題です。
光のように斜めの線が出てきたら、斜めの線の縦：横を考えましょう。今回は斜めの線の縦：横が80：100なので、４：５です。
棒の高さを縦、地面にできる影を横と考えればイチコロですね。

(２)は、棒の先端から壁(高さ２m)の部分に補助線を引き、横が３mの直角三角形を作ります。縦：横が４：５であることは当然変わりませんので、直角三角形の縦は３×４÷５より2.4mとなり、棒の高さは2.4＋２＝4.4ｍであることが分かります。

(３)は、(２)と同様に4.4mの棒の先端から影の一番上に補助線を引き、横が3.5ｍの直角三角形を作ります。縦：横が４：５であることを利用すると、直角三角形の縦は2.8mと分かります。影の一番上の高さより棒の先端までの長さが4.4m－2.8mとなるので、影の高さは1.6mであることが分かります。よって、３＋0.5＋1.6＝5.1ｍ。
大問５と同様、図２、図３は歪んだ図になっています。図形問題では図を見た目通りに信じないようにしましょう。

大問７　場合の数（色ぬり）

問題数：３
難易度：A，B，C

まずは、問題文のルールをしっかりと整理し、場合分けして解き進めていきましょう。(３)の２種類の芝アイスの通り数は、直接出すよりも、芝アイス全体の通り数－（１種類の芝アイスの通り数＋３種類の芝アイスの通り数）で出す方が楽でしょう。
今回の芝アイスの問題は解説記事を用意しておりますので、以下リンクより是非ご覧ください。

大問８　水そうグラフ

問題数：２
難易度：A，A

(１)は、グラフ問題。グラフ問題は、グラフが変化している所の原因を考えましょう。
今回は２分後に給水口Aを閉じ、同時に給水口Bを開け、①の時間に再び給水口Aを開け、18分～20分の間に水があふれ、20分後には給水口Aを閉じると共に排水口Cを開けます。最後に、26分後に給水口Bを閉じ、32分後に水槽の中の水は無くなります。
問題文とグラフを両方見て、グラフが変化している所の原因を考えてください。また、グラフ上にどの給水口、排水口が開いているか、閉じているかを書き込むことをお勧めします。(例：①～18分のグラフにはA＋Bと書き入れる）

(２)は、排水口Cが関係している20分～32分に着目すると、給水口Bは20分～26分の６分間給水し、排水口Cは20分～32分までの12分間排水し、結果として270L入っていた水が０Lにまで減少しています。こちらを利用して、排水口Cの１分間あたりの排水量を求めましょう。

大問９　平面図形（折り紙）

問題数：２
難易度：A，B

(１)は、図２の右上、左下の三角形を切り落とし、図３となりました。１辺８cmの折り紙を４回折ると図２の状態になるので、図３の状態から４回さかのぼりましょう。一気に最後までさかのぼるのではなく、１回１回どこが切り落とされているかをていねいに書き込み、さかのぼっていくことがミスなく正答するコツです。(切り落とされたところを斜線で表すなど工夫しましょう。)

(２)は、(１)の図３に対して１回ハサミを入れているので、(１)で求めた⑥の形を基準に考えると分かりやすいでしょう。
(１)と同じように図４の状態からさかのぼり、どこに切り目が入るのかを１回１回考え、問題用紙上の図に書き込めば、図形の面積や個数も簡単に求まります。

Kの考察

2017年度の第１回入試は問題の傾向に大きな変化はないものの、問題数が19問と多めでした。試験時間50分で19問ですので、大問４の規則性、大問７の場合の数など途中の問題で詰まってしまい、最後の大問９まで辿りつけなかった子も多いのではないでしょうか。

合格者平均点は62.1点と芝中学の過去入試の中では比較的低い点数となりました。19問中 A問題が12問(63%)、B問題が６問(32%)、C問題が１問(５%)で構成されていますので、合格・不合格の観点ではA問題をしっかり点数を稼ぎ、B問題を出来る限り取るという例年通りのスタンスで合格者平均点には達する事が出来たでしょう。

時間が足りなかった子は、問題を見た瞬間から書き出すまでの初動の速さを日々意識して取り組んでください。
また、大問１から順番に解くのではなく取り組みやすい問題から解くことや、大問の(２)(３)などで手が止まってしまう場合は潔く飛ばすなど入試特有のテクニックを過去問演習時や日々の模試で鍛えておくことも有効でしょう。

芝中学の過去問題集

芝中学関連情報

芝中学の算数分析｜過去問解説はコチラ