①から⑦までの番号のついた座席が横１列に並んでいます。人が座っている席のとなりには誰も座らないとします。
たとえば、①の席に人が座った場合②には誰も座らず、②の席に人が座った場合①と③には誰も座りません。このとき、次の問に答えなさい。① ② ③ ④ ⑤ ⑥ ⑦
(１) A、B、C、D ４人の座り方は何通りですか。
(２) A、B ２人の座り方は何通りですか。
(３) A、B、C ３人の座り方は何通りですか。
ラ・サール中学（2019年）
男子名門校のラ・サール中学より「場合の数」の問題です。レッツトライ！
場合の数は同校の頻出単元の１つなので、志望者はしっかりと対策をして入試に臨みましょう。
過去問解説記事の使い方は以下をご参照ください。
難度
Lv.３ 中学受験 難関校標準問題
中学受験 難関校の標準問題。難関校合格のために必要な標準問題を確実に正答する力をつけたい受験生や、合否を分ける問題を１問でも多く正答できるように得点力をアップさせたい中堅校志望の受験生にオススメ。
※偏差値の目安やその他難度の詳細などはコチラをご覧ください。
解説
(１) A、B、C、D ４人の座り方は何通り？
プロ家庭教師K人が座っている席のとなりには座れないので、①～⑦の席を４人で座るためには必ず 以下のような座り方になります。
×がついている席は座れないので、座ることのできる４席①、③、⑤、⑦に座ることになります。
よって、A、B、C、D の並び方を考えると４人での座り方は、４×３×２×１＝24通りです。
(２) A、B ２人の座り方は何通り？
AとBの２人のみで座る時、２人がとなり合わない座り方は何通りか？というのが(２)の問題設定です。
プロ家庭教師Kとなり合わない席の選び方を決めてから、AとBの順番を考えてみよう。
となり合わない席の選び方は、上画像の通り15通りになります。AとBの順番は（A、B）（B、A）の２通りなので、15×２＝30通りが答えになります。
プロ家庭教師K極端な①③から始めて１つずつ席をズラしていくのが数え漏れを防ぐポイントですね。
別解① A、Bがとなり合う座り方を除く
プロ家庭教師K「父，母，長男，次男，長女の５人が１列に並ぶとき、父と母がとなり合わない並び方は何通りあるか？」
こんな問題、塾のテキストでみんな解いたことがあるだろう。今回の問題も、この問題と同じように考え「全体の通り数」から「となり合う通り数」を引いて「となり合わない通り数」を求めることも出来ますね。
つまり、「何も制限が無い状態でのAとBの座り方」－「AとBがとなり合う座り方」＝「AとBがとなり合わない座り方」を利用して解くことが出来ます。
何も制限が無いとき、Aの座り方は７通り、Bの座り方は６通りなので、AとBの座り方は７×６＝42通り
AとBがとなり合う場合、となり合う席の選び方は①②、②③、③④、④⑤、⑤⑥、⑥⑦の６通り。AとBの順番は（A、B）（B、A）の２通りなので、AとBの座り方は６×２＝12通り
よって、A、B ２人の座り方は42－12＝30通りです。
別解② ６席の座り方を考え、AとBの間に空席を１つ入れる
となり合う、となり合わないを考えることなく、１席少ない６席でのAとBの座り方を考えます。その後、AとBが座っている間に誰も座っていない１席を入れ、７席にします。すると、AとBが座っている間に空席を１つ入れるので、その時の７席の座り方はAとBは必ずとなり合っていない状態になります。
例えば、６席の座り方が下画像のように（A，B，×，×，×，×）の場合は、AとBの間に空席を１つ入れ（A，×，B，×，×，×，×）、つまり、席①にA、席③にBが座っていることを表します。
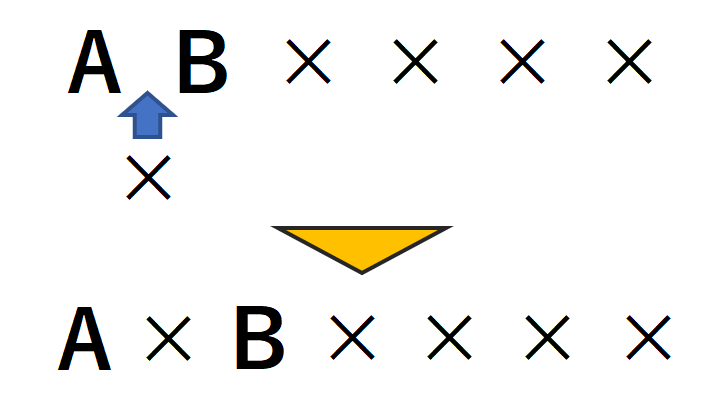
下画像のその他の例も見てみましょう。
（A，×，×，×，B，×）の場合は（A，×，×，×，×，B，×）
（×，×，B，A，×，×）の場合は（×，×，B，×，A，×，×）
先ほど書いたように、６席の座り方を考え、残りの空席１つをAとBの間に入れれば、AとBがとなり合わない７席の座り方になります。残りの１席は、AとBの間に入るように自動的に決定されるので、通り数には影響しません。通り数は６席の座り方がそのまま答えとなります。
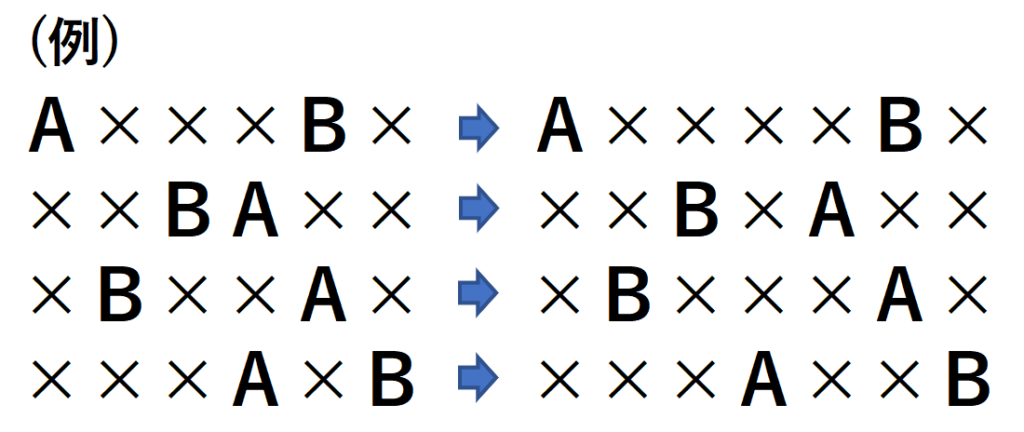
よって、Aの座り方は６通り、Bの座り方は５通りなので、答えは６×５＝30通りになります。
(３) A、B、C ３人の座り方は何通り？
プロ家庭教師K(２)の別解①と同じように、３人で座る時のとなり合わない席の選び方を考えてみましょう。
となり合わない席の選び方は、上画像の通り10通りになります。AとBとCの順番は３×２×１＝６通りなので、A、B、C ３人の座り方は10×６＝60通りが答えになります。
プロ家庭教師K極端な①③⑤から始めて、①③⑥⇒①③⑦というように、１つずつ席をズラしていくのが数え漏れを防ぐポイントですね。
別解① ５席の座り方を考え、AとB、BとCの間に空席を１つずつ入れる
(２)の別解②と同様に考えてみましょう。
(２)では、１席少ない６席でのAとBの座り方を考えましたが、今回は、A、B、Cの３人なので、２席少ない５席での３人の座り方を考えます。その後、座っている人の間に空席を１つずつ入れて、７席の座り方を考えます。すると、人が座っている間に誰も座っていない１席を１つずつ入れるので、７席の座り方は誰もとなり合わない状態になります。
例えば、５席の座り方が下画像のように（A，B，C，×，×）の場合は、AとB、BとCの間に空席を１つずつ入れ、（A，×，B，×，C，×，×）、つまり、席①にA、席③にB、席⑤にCが座っていることを表します。
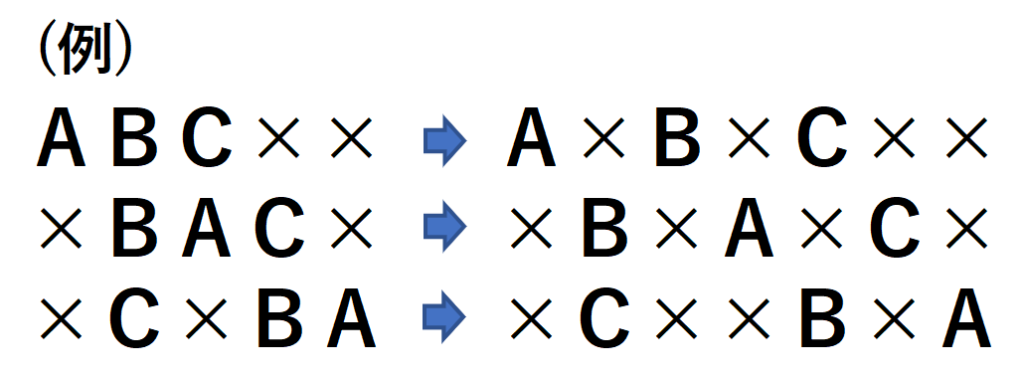
よって、５席の座り方を考え、座っている人の間に空席を１つずつ入れれば、A、B、Cの３人それぞれがとなり合わない７席の座り方になります。空席を入れる場所は自動的に決定されるので、通り数には影響しません。通り数は５席の座り方がそのまま答えとなります。
よって、Aの座り方は５通り、Bの座り方は４通り、Cの座り方は３通りなので、答えは５×４×３＝60通りになります。
Kとピヨまるの談話室
ピヨまる冒頭の画像左上に「時事問題」マークがついていますが、この問題のどの部分が時事問題なんですか？ただの場合の数に見えますけど？
プロ家庭教師K今回は2019年に出題された問題だが、「となりに座ることが出来ない」という条件は、現在(2021年)の過ごし方と同じだよね。よって、コロナ関連問題として時事問題扱いにしている。
ピヨまるほぉ。コロナ関連ですか。確かに。
今回はラーメン店のようなカウンタータイプの席ですが、他にどのような問題が考えられますかね？
プロ家庭教師Kそうね。例えば、以下のように８人用の対面型の座席で「人が座っている席のとなりに座ってはいけません」に加え、「人が座っている席の正面に座ってはいけません」という条件なども考えられるかな。
自分で作問してみるのも良いトレーニングになるよ。
こちらの記事もオススメ☆
・ラ・サール中学の算数分析／過去問解説はコチラ
・過去問解説記事の一覧はコチラ
・場合の数の過去問解説はコチラ
・その他の難関校標準問題（★★★☆☆）はコチラ
