場合の数｜色ぬり問題（芝中学 2017年）

次の問いの□をうめなさい。

カズオ君は学園祭でアイスクリーム屋をやることになりました。味はチョコ，バニラ，イチゴの３種類です。スプーンですくって最大４つのアイスクリームを縦に重ね，”芝アイス”として売ることにしました。同じ味が複数あってもよいこととし，さらに重ねる順番をお客さんは選ぶことができます。また，重ねる順番が異なる場合は異なるものとして考えます。

（１）芝アイスは全部で□通りあります。
（２）味が３種類の芝アイスは全部で□通りあります。
（３）味が２種類の芝アイスは全部で□通りあります。

例　アイスクリームを２つ重ねて作った場合の”芝アイス”

　　

芝中学（2017年）

男子難関校の芝中学より場合の数の問題です。学園祭で売られているアイスクリームの問題でその名も”芝アイス”。本当に芝中学の文化祭で売ってそうですね。どうなんでしょう？
過去問解説記事の使い方は以下をご参照ください。

難度

解説

（１）芝アイスは全部で何通りか？

まずは、基本ルールを確認しておきましょう。
今回の基本ルールは以下の４つとなります。このルールに矛盾していないか常に気を付けて解き進めていってください。

1. アイスは最大４つ重ねることができる
2. アイスの味は３種類
3. 同じ味のアイスが複数あってもよい
4. 重ねる順番が異なる場合は異なる芝アイス

（１）は芝アイスが全部で何通りか？
この問題はアイスを重ねる個数やアイスの味に制限はありません。つまり、アイスは最大４つ重ねることができますし、１つでも２つでも、３つ、４つでもOKであることが分かりますね。
アイスが１個、２個、３個、４個の場合でそれぞれ考えていきます。

味のないアイスにそれぞれ味をつけていくイメージですので、考え方としては色ぬり問題と同じで良いでしょう。ただ、今回の芝アイスは、一般的な色ぬり問題と異なり、となり合う味（色）が同じでもOKですので、その点は注意してください。

１個のとき：３通り
２個のとき：３×３＝９通り
３個のとき：３×３×３＝27通り
４個のとき：３×３×３×３＝81通り

よって、３＋９＋27＋81＝120通りです。

A.120

（２）味が３種類の芝アイスは何通りか？

味が３種類の芝アイスですので、３つ重ねたアイスか、４つ重ねたアイスを考えます。（１つ、２つのアイスでは味を３種類入れることは不可能ですよね。）

３つ重ねたアイスのとき

３つ重ねたアイス、かつ味が３種類なので、重ねた３つのアイスそれぞれが異なる味である必要があります。（１）と違い、今回はとなり合う味が同じであってはならないということですね。

よって、３×２×１＝６通り

４つ重ねたアイスのとき

４つ重ねたアイス、かつ味が３種類なので、重ねた４つのアイスのうち、２つが同じ味、あと２つは別々の味でなくてはなりません。４つのアイスの中で、同じ味のアイス２つがどれかを決めれば、残り２つは別々の味と確定しますので、まずは同じ味のアイス２つの場所を考えます。
コーンは問題と関係ないのでそろそろ省きますか。（決して描くのが面倒くさいからじゃないぞ・・）

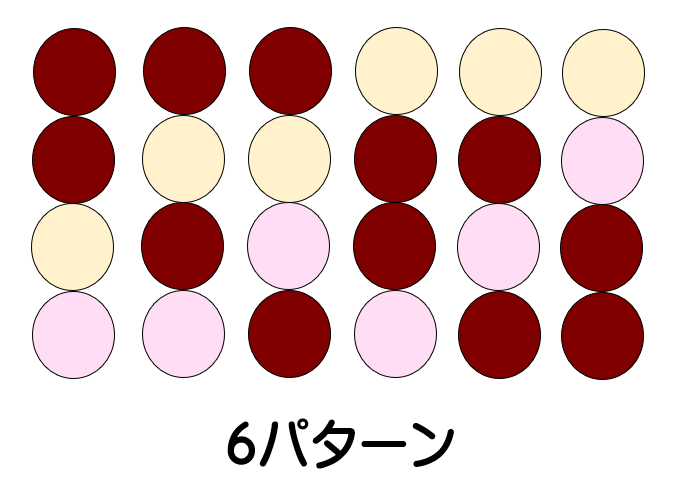
考え方は「４つの中から同時に２つを選ぶ」と同じですので、（４×３）÷（２×１）＝６より、「アイス２つが同じ味で、残りのアイスは別々の味であるパターン」は６パターンあることが分かります。（上画像参考）

また、６パターンいずれにおいても、味は３種類ですので、味の決め方は３×２×１の６通りあります。
よって、アイスを４つ重ね、味が３種類の芝アイスは６×６＝36通りとなります。

味が３種類の芝アイスは６＋36＝42通り。

A.42

（３）味が２種類の芝アイスは何通りか？

ラストは２種類の芝アイス。さて、（１）では味が１、２、３種類すべての芝アイスを求め、（２）では味が３種類の芝アイスを求めましたね。まだ求めていない芝アイスは「味が２種類の芝アイス」と「味が１種類の芝アイス」です。どちらの芝アイスが通り数を出しやすいでしょうか？

味が１種類のときは、重ねたアイスが何個でも味は１種類なので、チョコ、バニラ、イチゴの３通りとなります。よって、４×３＝12通りとなります。

全体の通り数は（１）の答えより、120通り。
味が１種類のときは12通り、３種類のときは42通りですので、味が２種類の芝アイスは120－（12＋42）＝66通りとなります。

A.66

Kとピヨまるの談話室

こちらの記事もオススメ☆

・芝中学の算数分析 / 過去問解説はコチラ
・過去問解説記事の一覧はコチラ
・場合の数の過去問解説はコチラ
・その他の難関校標準問題（★★★☆☆）はコチラ

芝中学の過去問題集