次の文章を読んで,【ア】から【カ】を適切にうめなさい。
Aさん,Bさん,Cさん,Dさん,Eさんの5人がクリスマスプレゼントをそれぞれ1個ずつ用意し,Aさんの家に集まってクリスマスパーティーをしました。Aさんは手袋,Bさんはマフラー,Cさんはクッキー,Dさんはイチゴ,Eさんはチョコレートをプレゼントとして持ってきました。
プレゼントはそれぞれ同じ箱に詰め,誰が何をもらえるか分からないようにしてプレゼント交換をしました。交換後に5人は,他の人に見えないようにして箱を開け,全員が,もらったプレゼントは自分の用意したものではないことを確認しました。そして,次のように言いました。Aさん「私がもらったのはお菓子だったよ。」
Bさん「私の好きな食べ物だったから満足しているわ。」
Cさん「私も欲しいものだった。今度,身に着けて遊びに行こうかな。」
Dさん「私がもらったのはAさんからのプレゼントじゃないよ。」
Eさん「私も好きな食べ物だったよ。」すると,これを聞いていたAさんのお母さんが次のように言いました。
お母さん「Cさんは【ア】,Dさんは【イ】をもらったでしょう。」
Cさん「その通りです。」
Dさん「私も,その通りです。では,残りの3人が何をもらったのかも分かりますか。」
お母さん「自分がもらったプレゼントは知っているから,残りの3人の中に,自分以外の2人が何をもらったか分かる人がいるかもしれない。」このことを聞いた後,【ウ】さんとAさんが同時に
「他の2人が何をもらったか分かった。」
と言いました。お母さんはそれを聞いて,
浦和明の星女子中学(2014年)
お母さん「Aは【エ】を,Bさんは【オ】を,Eさんは【カ】をもらったね。」
と言いました。
Aさん,Bさん,Eさん「その通りです。」
女子名門校の浦和明の星女子中学より「推理と論証」の問題です。
名探偵になったつもりで各条件から分かる情報をまとめて、答えを求めましょう。推理ですので学年問わずトライしてみてください!
過去問解説記事の使い方を読んだ上で、算数の志望校対策や、得点力アップ、弱点補強にご活用ください。

問題の難度
Lv.3 中学受験 難関校標準問題
中学受験 難関校の標準問題。難関校合格のために必要な標準問題を確実に正答する力をつけたい受験生や、合否を分ける問題を1問でも多く正答できるように得点力をアップさせたい中堅校志望の受験生にオススメ。
※偏差値の目安やその他難度の詳細などはコチラをご覧ください。
解説
問題文の条件から何が読み取れるのかを考えよう
推理と論証の問題です。問題文の条件から読み取れる情報を用いて、確定している部分とまだ不明な部分を整理しましょう。
そして、不明な部分を推理しながら解き進めていくのが基本的な解き方の流れです。
 プロ家庭教師K
プロ家庭教師K今回は5人がプレゼントを持ち寄って、プレゼント交換する問題です。情報量も多いので、頭の中ですべて考えるのではなく、表を作って、問題文の情報や新たに判明した情報を反映させていきましょう!
「全員がもらったプレゼントは自分の用意したものではない」ことを確認していますので、まずは自分が持ってきたプレゼントの所に×マークを付けましょう。
Aさんは手袋、Bさんはマフラー、Cさんはクッキー、Dさんはイチゴ、Eさんはチョコレートに×を付けます。
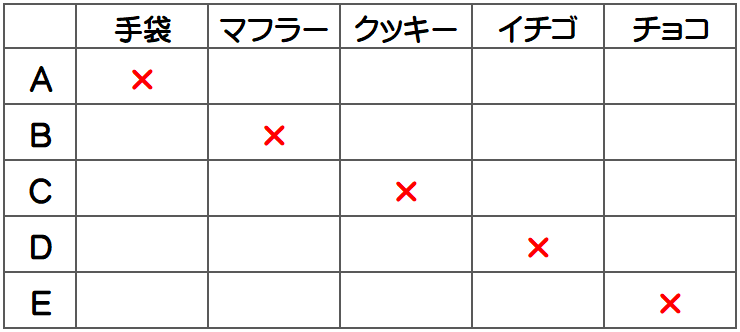
次に、みんなのコメントに着目しましょう。
太字の部分がコメントから分かる内容です。
・Aさん「私がもらったのはお菓子」
→お菓子なので、Aさんはクッキーかチョコレート
・Bさん「私の好きな食べ物だったから満足」
→食べ物なので、Bさんはクッキーかイチゴかチョコレート
・Cさん「私も欲しいものだった。身に着けて遊びに行こうかな」
→身に着けるものなので、Cさんは手袋かマフラー
・Dさん「私がもらったのはAさんからのプレゼントではない。」
→Dさんがもらったのは、手袋ではない
・Eさん「私も好きな食べ物だった」
→食べ物なので、Eさんはクッキーかイチゴ(チョコレートはEさん自身が持ってきたので不可)
 プロ家庭教師K
プロ家庭教師K上記を1つずつ表に反映させましょう!赤い×マークが新たにつきます!
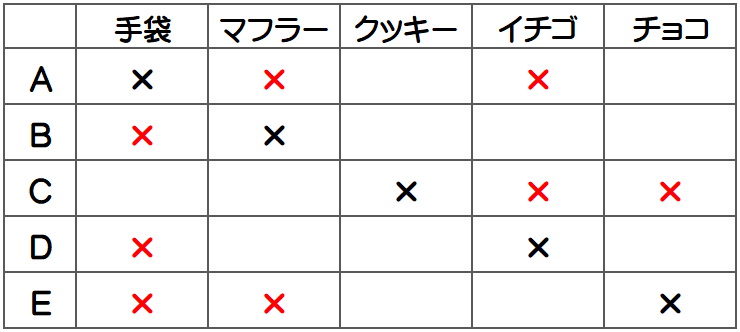
さて、ここまでを聞いて、Aさんのお母さんが言いました。
「Cさんは【ア】,Dさんは【イ】をもらったでしょう?」
 ピヨまる
ピヨまるこえぇぇ~!
何者なんですか・・Aさんのお母さんは・・・。
 プロ家庭教師K
プロ家庭教師Kわ、分からん。ただ者ではないことは分かるが・・。
とりあえず、次に進もう。
Aさんのお母さんは、CさんとDさんの話をしているので、CさんとDさん関連の情報を確認しましょう。表を見てみると、Cさんは手袋・マフラーのどちらかをもらうことが確定しており、かつ手袋・マフラーはAさん、Bさん、Eさんはもらうことが出来ないことが分かります。
つまり、手袋・マフラーはCさんとDさんの2人でもらうことが確定となり、手袋に×がついているDさんはマフラーをもらい、Cさんは手袋をもらうことになります。
すかさず、表にも〇、×マークを反映!
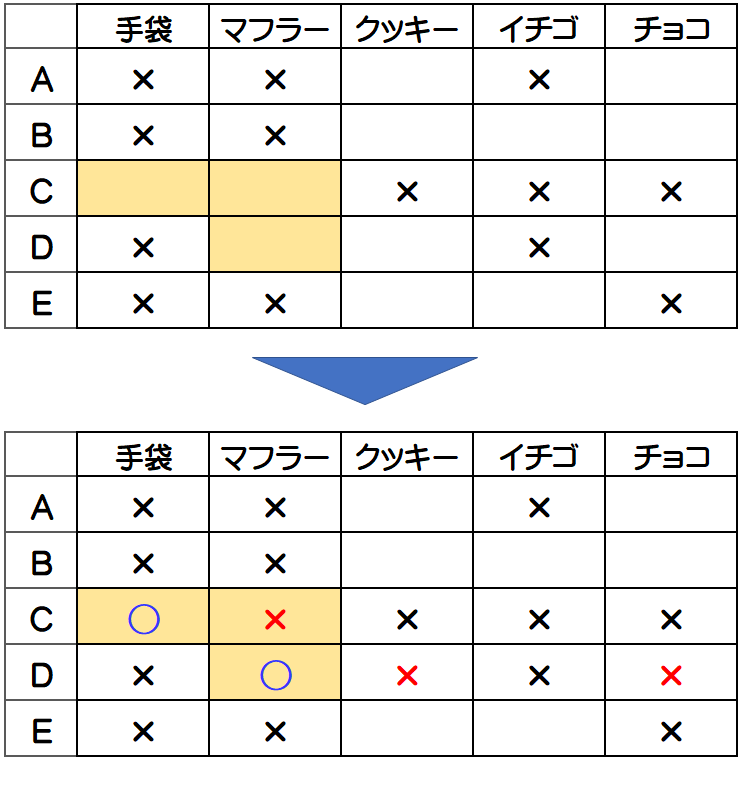
次に、Aさんのお母さんが「あなた達は自分自身がもらったプレゼントは知っているから、残りの3人の中に自分以外の2人が何をもらったか分かる人がいるかもしれないわね。んふふふふ。」と絶妙なアドバイスを出したところ、【ウ】さんとAさんが同時に「他の2人が何をもらったか分かった。」と答えました。
ここから何が分かるでしょうか?
まず、Aさんは「(自分自身がもらったプレゼントを考えた上で)他の2人が何をもらったか分かった」と言っているので、Aさんがクッキー、チョコレートのどちらをもらったのかを考えましょう。
表より、Aさんがクッキーをもらう場合は、Eさんはイチゴをもらうことが確定し、自動的にBさんはチョコレートをもらうことが決まります。
Aさんがチョコレートをもらう場合は、Bさん、Eさんのどちらがクッキー、イチゴをもらうかは確定となりません。よって、Aさんはクッキー、Bさんはチョコレート、Eさんはイチゴをもらうことが決まります。
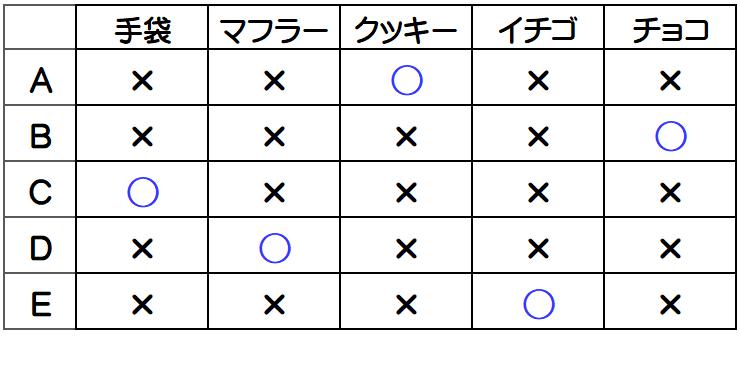
では、「他の2人が何をもらったか分かった!」と言ったのは、BさんとEさんのどちらでしょうか?
まず、Bさんの立場になってみると、自分はチョコレートをもらっていることが分かっています。すると、お菓子をもらったAさんはクッキーをもらうことが確定し、自動的にEさんは残りのイチゴをもらうことが確定します。
よって、他の2人がもらったプレゼントが分かるのはBさんです。
 プロ家庭教師K
プロ家庭教師KEさんは自分はイチゴをもらっていることが分かるだけで、Aさん、Bさんがクッキーとチョコレートのどちらをもらうかは分からないよね。
Kとピヨまるの談話室
 ピヨまる
ピヨまるこの問題のポイントは、Aさんのお母さんが何者か?という点ですね!
 プロ家庭教師K
プロ家庭教師Kんなわけねえ。気になるけどね。うん、気になるけど。
推理の論証に限らず、問題文から読み取れる情報が多いときは、頭の中だけで解かず、必要に応じて表やメモを使って解き進める。これがポイントかな。
 ピヨまる
ピヨまるAさんのお母さんの頭の回転の速さは並じゃないですよ。表を使うどころか、頭の中ですべて処理し、何ならアドバイスを出して、途中から場を仕切っていますからね。いや~、一体何者なんでしょうか。何だか楽しくなってきましたよ。
ん?何かしゃべってましたか?
 プロ家庭教師K
プロ家庭教師Kは・な・し・き・け。
こちらの記事もオススメ☆
・浦和明の星中学の算数分析/過去問解説はコチラ
・過去問解説記事の一覧はコチラ
・推理と論証の過去問解説はコチラ
・その他の難関校標準問題(★★★☆☆)はコチラ

