２以上の整数に対して、１になるまで以下の操作を繰り返します。
・偶数ならば２で割る
・奇数ならば３倍して１を加える例えば、６であれば、次のような８回の操作によって１になります。
６→３→10→５→16→８→４→２→１
このとき、次の□に適当な数を入れなさい。
(１) 11は□回の操作で１になります。
(２) 12回の操作で１になる整数は全部で□個あります。
慶應義塾中等部（2021年）
名門私立 慶應義塾中等部より「規則性」の問題です。過去問解説記事の使い方は以下をご参照ください。
問題の難度
Lv.4 中学受験 難関校応用問題
中学受験 難関校の応用問題。難関校志望の生徒は、本レベルの問題演習を通じて、合否を分ける応用問題を１問でも多く正答できるように得点力をアップさせましょう。
※偏差値の目安やその他難度の詳細などはコチラをご覧ください。
解説
(１) 11は何回の操作で１になる？
(１)はルールが決まっている問題の定番、「まずはルール通りやってみよ問題」です。やってみましょう！
はじめは11で奇数なので、３倍して１足すところからスタートします。すると、11×３＋１＝34となり、次は偶数なので２で割り、34÷２＝17となります。
同様に進めると、11から始まり、
・11×３＋１＝34
・34÷２＝17
・17×３＋１＝52
・52÷２＝26
・26÷２＝13
・13×３＋１＝40
・40÷２＝20
・20÷２＝10
・10÷２＝５
・５×３＋１＝16
・16÷２＝８
・８÷２＝４
・４÷２＝２
・２÷２＝１（14回目）
プロ家庭教師K実際に解く際には、上記のようにひとつひとつの計算式を書くのではなく、11→34→17→52→26→13→40→20→10→5→16→8→4→2→1というように計算結果のみをメモしていきましょう。
以上のように、14回の操作で１になることが分かります。回数が多いので、数え間違いしないようにしっかりと指差し確認をしましょう。(操作の回数なので、→を数える）
(２) 12回の操作で１になる整数は何個？
プロ家庭教師K(１)は「はじめの整数が与えられて何回の操作で１になるか？」でしたが、今回は「操作の回数が与えられて、はじめの整数の通り数を出す」問題ですね。どこから解こうか？
ピヨまるう～ん。操作のルールは分かっているので、
・はじめの整数を２にしたら操作は何回になるか
・はじめの整数を３にしたら操作は何回になるか
・はじめの整数を４にしたら操作は何回になるか
…と続けていって、「はじめの整数と操作の回数に規則性がないのかを探す」というのはどうでしょう？
プロ家庭教師K自分で試していって規則性を探すのは考え方の１つとしてはあるね。
ただ、今回の問題は、はじめの整数から始めてしまうと、分かっている情報が極めて少ないよね。規則性が見つかるまで地道に続けないといけないし、そもそも何個まで検証すればいいのかも不明だから、膨大な時間が掛かりそう。
ピヨまるう～ん。分かっている情報といっても、「12回の操作」と「最後は１になる」しか分かってな・・・
あっ、最後からさかのぼればいいのか！
今回の問題では、はじめの整数が何であるか？はじめの整数は何通りであるか？は分かりませんが、「12回の操作で１になる」ことは確定しています。最後が１であるという確定情報からさかのぼって解き進めていきましょう！
操作の内容は、①偶数ならば２で割る、②奇数ならば３倍して１を加えるの２つ。
最後は１で終わるので、12回目の操作は、操作①であることが確定します。また、２で割って最後は１になるため、12回目の操作を行う前の整数は２であることも確定します。
もう１つさかのぼってみましょう。11回目の操作をして２になるので、操作を行前の整数は、操作①の場合は２×２＝４。操作②の場合は（２ー１）÷３＝\(\large{\frac{１}{３}}\)で分数となるのでNGです。つまり、11回目の操作は操作①のみがOKで、操作前の整数は４で確定です。
10回目の操作をして４になる整数は、操作①の場合は４×２＝８。操作②の場合は（４ー１）÷３＝１で整数となるので、OK・・ではありません。今回のルールは１になるまで操作を続けることですので、１つ前が１となることはあり得ません。（１となった段階で操作が終了なので、１つ前の整数が１となることは無い）
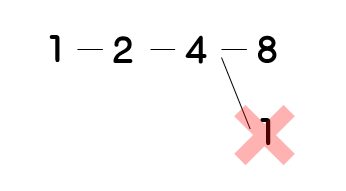
プロ家庭教師Kさて、ここから最初の操作までさかのぼっていきますが、操作①は必ず出来るので、操作①を12回分行う場合の樹形図を先に書いてしまいましょう。
さて、最後の整数１から３回さかのぼってきましたが、ひとつ前の操作①，操作②が出来るか否かには決まりがあります。
操作を１回して整数Nになったと考える場合、
・操作①を行い、整数Nとなった時
→ひとつ前の数は、N×２ ※N×２は必ず偶数となるので、操作①は毎回出来る
・操作②を行い、整数Nとなった時
→ひとつ前の数は、（N－１）÷３ ※操作②をする時は必ず奇数なので、（N－１）÷３が奇数になればOK
あとは、決まり通りに計算ミスや抜け漏れの無いように樹形図を完成させましょう。
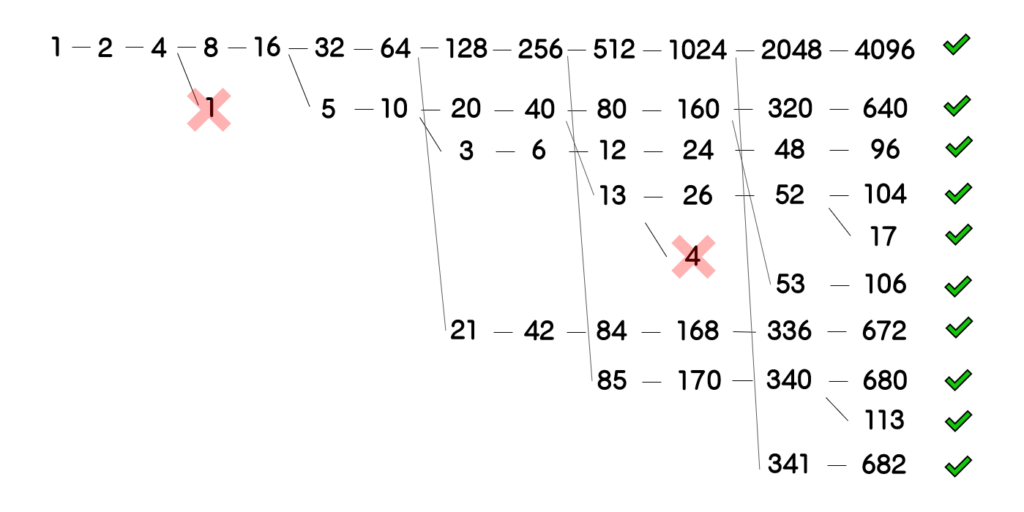
ピヨまる操作ごとに数が縦１列に並んでいますが、これは何か意図があるのでしょうか？
プロ家庭教師Kある。余白を取らずに細かくグチャグチャに書いて間違えたり、操作の回数と数を縦１列に書かずに数えモレをしたり、樹形図は数え間違いをする奴が非常に多い。縦のラインをそろえることで、数えモレをするリスクを低減させましょう。
今回は、✔の通り、10個が答えです。
算数は分かっている情報が多い所から解き始める！
Kとピヨまるの談話室
ピヨまる今回のブログタイトルで質問なんですけど、規則性の後に「コラッタ予想」と書いてありますが、何ですかこれ？
プロ家庭教師Kいや、コラッツね。コラッタはポケモン。コラッツ予想は、1937年にドイツの数学者コラッツが提示した問題で、現在も未解決なんだよ。（※2021年６月時点）
内容は「整数ｎが偶数の場合、ｎを２で割る」「整数ｎが奇数の場合、ｎに３を掛けて１を足す」という操作を繰り返すと、どのような整数ｎを選んだとしても、必ず１に達する（そして、１→４→２→１というループになる）という予想だね。本問題とまるっきり同じ設定なわけよ。
ピヨまるほぇぇ、70年以上経っているのに未解決なんですね。なんか壮大な話だなぁ。
こちらの記事もオススメ☆
・慶應義塾中等部の算数分析／過去問解説はコチラ
・過去問解説記事の一覧はコチラ
・規則性の過去問解説はコチラ
・その他の難関校応用問題（★★★★☆）はコチラ
