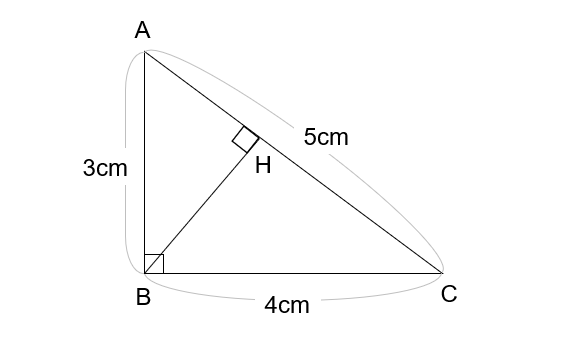
下の図形について、あとの各問いに答えなさい。
① BHの長さは何cmですか。
② 三角形ABCを辺ACを軸にして回転させた立体と、辺ABを軸にして回転させた立体の体積の比を、最も簡単な整数の比で書きなさい。
共立女子中学(2014年)
共立女子中学より立体図形の回転体の問題です。色々なポイントの詰まった学習効果の高い問題ですので、回転体を1度でも学んだことのある中学受験生はぜひトライしてみてください!
難度
Lv.2 中学受験 標準問題
全受験生にオススメの中学受験算数の標準問題をまとめています。シンプルな問題設定が多いため、算数の各単元のポイント整理にも有効です。本レベルの演習を通じて、受験算数の基礎固めを行いましょう。
※偏差値の目安やその他難度の詳細などはコチラをご覧ください。
解説
① BHの長さは何cmですか?
辺BHの長さを求める問題。
まだ回転していないので、①は平面図形の問題です。
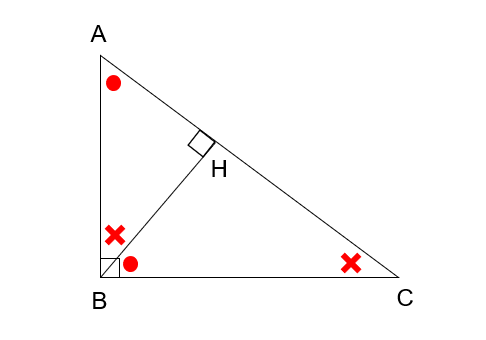
上記のように●、×の角度を置いてあげると、3つの角度がそれぞれ同じなので、△ABCと△AHBと△BHCが相似であることが分かります。以下、相似を使用するときの注意点も重要ですので、一読しておきましょう。
 プロ家庭教師K
プロ家庭教師K問題文に載っている図が正しく書かれているとは限りません。
相似を使う時は、パッと見で判断してはダメ。きちんと角度や辺の比を確認した上で、相似を使いましょう。
△ABC、△AHB、△BHCが相似なので、タテヨコナナメの3辺の比はすべて等しいことが分かります。△ABCの3辺の長さは図より3cm、4cm、5cmなので、3辺の比は3:4:5になります。
また、△ABCと△AHBのナナメの辺(斜辺)は5cmと3cmですので、△ABC、△AHBの相似比は5:3であることが分かります。
△AHBのBHは、△ABCのBCと対応する辺なので、BH=AB×\(\large{\frac{4}{5}}\)=3cm×\(\large{\frac{4}{5}}\)=2.4cmとなります。
 プロ家庭教師K
プロ家庭教師Kパッと見で相似・合同と確定してはいけませんが、今回のように直角三角形が組み合わさった相似は「よくある相似」の1つです。
見た瞬間「はいはい、またこのパターンね!ありがとうございまーーす!」と思えるレベルにしておきましょう。
(2)辺ACを軸にした回転体と辺ABを軸にした回転体の体積比は?
さて、いよいよ回転体です。
回転体はまずどんな立体になるのかをイメージしましょう。回転体を習って間もない子や、回転体に苦手意識のある子は実際に立体を描く癖をつけておいてください。
回転体は、以下のように軸となるAC、ABに対し、対応する点●をそれぞれ取って、その点と各頂点を結び、立体図形を描くとキレイにまとまります。
左の立体がACを軸にして回転させた立体、右の立体がABを軸にして回転させた立体です。
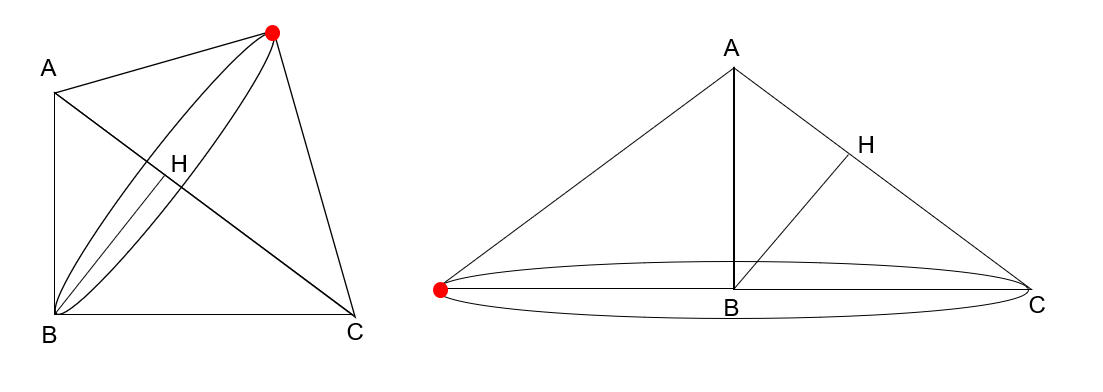
すると、ACを軸にして△ABCを回転すると半径が2.4cm(設問1で求めたましたね)、高さが上下(AHとHC)合わせて5cmの2つの円すい。ABを軸にして△ABCを回転すると半径が4cm、高さが3cmの円すいが出来上がります。
それぞれの円すいの半径は2.4cmと4cmなので、簡単な比にすると3:5、高さは5cmと3cmなので、比はそのまま5:3。
よって、「三角形ABCを辺ACを軸にして回転させた立体と、辺ABを軸にして回転させた立体の体積の比」は、3×3×5:5×5×3=45:75=3:5になります。
 プロ家庭教師K
プロ家庭教師K×3.14や÷3などの共通部分は体積比に影響を与えないので、はじめから除きましょう!
Kとピヨまるの談話室
 ピヨまる
ピヨまる僕は(2)は実際の体積を出しました。
2.4cm×2.4cm×3.14×5cm÷3:4cm×4cm×3.14×3cm÷3を比に直して3:5になり、答えは合っていましたけど、計算が大変でしたね。
半径や高さも比に直して、求めれば良かったんですか。トホホのホ…。
 プロ家庭教師K
プロ家庭教師K今回の問題で聞かれているのは「実際の体積」ではなく「体積比」なので、半径も高さも比に直してから、計算で良いよ。
また、解説内のコメント通り、体積比に影響を与えない共通部分(今回は×3.14、÷3)を削ることなどもスピードアップのコツだね。
こちらの記事もオススメ☆
・共立女子中学の算数分析/過去問解説はコチラ
・過去問解説記事の一覧はコチラ
・立体図形(回転体)の過去問解説はコチラ
・その他の中学受験標準問題(★★☆☆☆)はコチラ