芝中学の算数分析と対策（2018年第1回）

男子難関校の芝中学の算数分析記事です。今回の過去問分析対象は「2018年第１回入試」となります。芝中学算数の傾向と対策方法を知り、合格に向けて是非ご活用ください。

芝中学 2018年入試結果

配点・試験時間

• 国語　100点（50分）
• 算数　100点（50分）
• 社会　75点（40分）
• 理科　75点（40分）

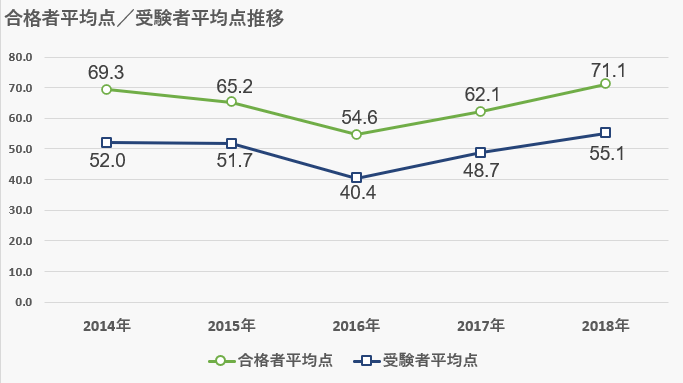
合格者平均点・受験者平均点

• 受験者平均点－55.1点
• 合格者平均点－71.1点

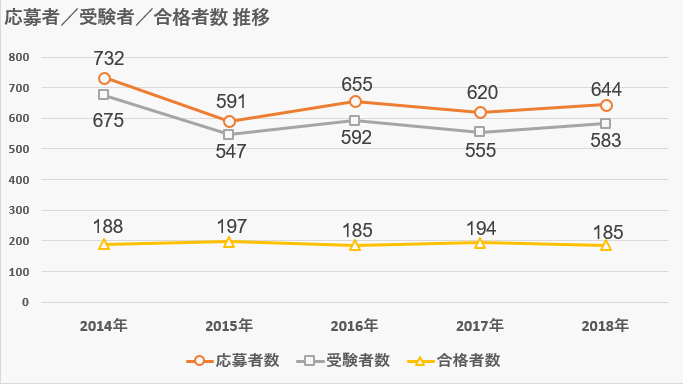
受験者数・合格者数

• 募集者数－150人
• 応募者数－644人
• 受験者数－583人
• 合格者数－185人

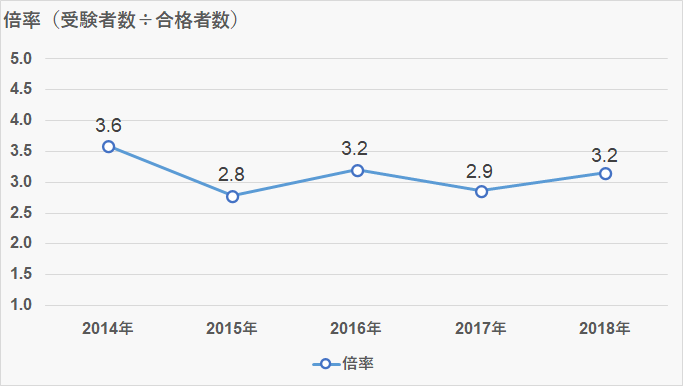
実質倍率

• 倍率：3.2倍

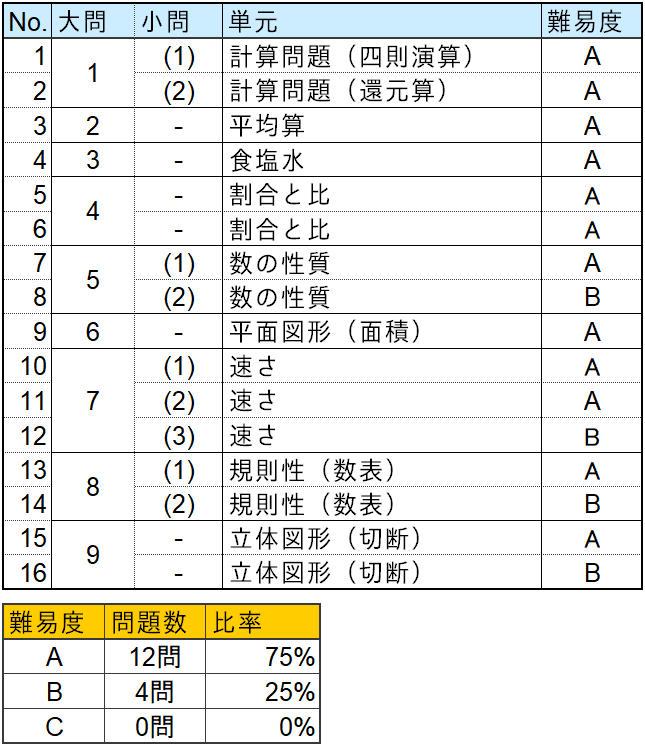
問題別難易度分析

【難易度説明】
A：芝中学合格のために正答したい問題
B：合否を分ける差がつく問題
C：発展問題（間違えても差がつかない）

問題別攻略のポイント

大問１　計算問題

問題数：２
難易度：A，A

(１)　四則演算

例年出題されている標準的な計算問題です。最後まで終わってから計算問題を検算する時間はほとんどの子が取れません。不安な計算は２度行うなど１つ１つの計算をていねいに取り組み、きっちり正答しましょう。

(２)　還元算

こちらも標準的な計算問題です。例年通り、芝中学の計算問題は答えを出すまでのステップがそれなりに多く、途中の計算や通分・約分などを間違えると当然正答できません。
また、小数、分数どちらで計算するのがいいかも臨機応変に対応しましょう。例えば、今回は最後の()内を小数で計算すると4.6となり、{}内が10であることが容易に分かります。

例年出題されている標準的な計算問題です。最後まで終わってから計算問題を検算する時間はほとんどの子が取れません。不安な計算は２度行うなど１つ１つの計算をていねいに取り組み、きっちり正答しましょう。

大問２　平均算

問題数：１
難易度：A

基本的な平均算です。単純に全て足してから10で割るか、15を基準に差だけ考えるか方針を立ててから始めましょう。また、15.01と15.99など綺麗に計算できる部分をまとめるのは基本テクニックです。
この問題に関しては、重さの平均を求める問題ですが、結局は単なる計算問題であることに皆気付くと思います。気付いた瞬間、「単なる計算問題なのだから、絶対に正答して点を稼がなければ！」という気持ちに切り替え、ていねいに取り組むようにしてください。

大問３　食塩水

問題数：１
難易度：A

基本的な食塩水の問題です。２つの容器の中での単純なやり取りの問題ですので、ビーカー図でよいでしょう。食塩水は「食塩水の重さ」「食塩の重さ」「濃度」の３要素から成ります。３要素の問題は２つの要素が分かっていれば、当然もう１つも計算で出せるので、その点に着目してビーカーの中身を埋めていきましょう。

大問４　割合と比

問題数：２
難易度：A，A

標準的な割合と比の問題です。最も少ない金額を持つC君を基準(①)にしてA君、B君の金額を比で表して解きましょう。B君はC君の２倍より200円少ないので、②－200円。A君はB君の３倍より700円多いので、B君×３＋700＝(②－200)×３＋700＝⑥－100円となります。
式の展開で解ける子は式で、厳しい場合は線分図を描いて３人の金額を比べましょう。

大問５　数の性質

問題数：２
難易度：A，B

０が何個続くのか問題です。塾のテキストでよく見るのは１から30まで連続した整数の積ですが、本問題は18から30までの整数の積となっており、問題を少しひねってきていますね。
×５は５の倍数にしか現れませんので、20、25、30のみ考えましょう。

(２)では４で何回割り切れるかを聞かれています。×２が２個あれば４で１回割れるので、×２の個数を数えていきましょう。×２は２の倍数にしか現れませんので、偶数である2006、2008、2010、2012、2014、2016、2018のみ着目してください。奇数は不要。
また、偶数全てを素因数分解するのはナンセンス。2006は２×1003(奇数)となるので、2010、2014、2018も２×奇数の形であり、×２の個数は１個しかないことが分かります。残った偶数の2008、2012、2016も倍数判別法で４の倍数なのか、８の倍数なのかを判断しながら工夫して×２の個数を数えていきましょう。
また、４で何回割り切れるか？なので、最後に÷２をすることを忘れずに。

詳しい解説は以下記事をご覧ください。

大問６　平面図形（面積）

問題数：１
難易度：A

芝中学では例年平面図形の問題が出されておりますが、本問題のレベルは高くありません。１辺１cmの正三角形を基準に相似比、面積比を使いながら、全体の面積比を出しましょう。
ただ、今回の図形問題も△EIGや△HEF、△HICを見た目で正三角形と判断するのではなく、しっかり問題文の平行の条件を確認してから、正三角形と判断するようにしてください。

大問７　速さ

問題数：３
難易度：A，A，B

典型的な速さのつるかめ算です。余裕のよっちゃん、余裕のよしこですね。
芝中学の志望者は、問題文を一読した瞬間、つるかめ算だと気付けるようなレベルに仕上げておきましょう。

(２)は264kmの高速道路を時速80kmで進むときの所要時間は3.3時間(＝198分)だが、18分短い180分で進むには時速何kmにすればいいですか？というだけです。
距離と時間が出ているので、速さは即出せるでしょう。距離が同じなので、逆比を使ってもいいですね。

(３)は(１)と同様、速さのつるかめ算です。ただ、(１)と比べ計算が複雑になっており、きっちり正答できるか否かで差がつく問題と言えるでしょう。
１つの試験の中で同じ考え方をする問題が出されることは珍しく、少し拍子抜けでもありますが、文章題においても複雑な計算を時間内に正確に出来るかを見られているのだと思います。

大問８　規則性（数表）

問題数：２
難易度：A，B

数表問題です。少し変則的ですが、まずはどのような周期(ルール)で進んでいるのかを確認しましょう。
１行１列目が空白、２列～７列目まで１～６で進み、折り返します。２行７列目が空白、６列～１列目まで７～12で進みます。そして、同じ進み方を繰り返していきます。
１～６までではなく、１～12までを１周期として考え、解き進めてください。繰り返す範囲がどこからどこまでなのか考えることが重要です。

(２)は２行を１周期として考えていきます。５列目の数の和を聞かれているので、２行ずつまとめて、和がどう増えていくのか確認してみましょう。

１行～２行は、４＋８＝12
３行～４行は、16＋20＝36
５行～６行は、28＋32＝60
というように、５列目の数を２行１周期に考えると、和は最初12で24ずつ増える等差数列になることが分かります。あとは等差数列の和の公式を用いて、解き進めてください。

大問９　立体図形（切断）

問題数：２
難易度：A，B

標準的な立体切断の問題です。
まずは、同じ面上の２点を結ぶので、点Aと点C、点Bと点Cを結びます。次に、BCが引かれた立方体の左面と向かい合っている右面に、BCと平行な線AEを引きます。すると、DEが1.5cmとなることが分かります。しっかりと正答し、得点を取りたい問題です。

点Dを含む立体の体積は、ACをAの方向、BCをBの方向に延長し、大きな三角すいを考え、立方体から点Dを含まない立体を除いて、点Dを含む立体の体積を出すのが一般的な解き方でしょうか。
または、AEをEの方向に延長して、縦３cm×横３cmの正方形(立方体の底面と同じ)を底面、高さ４cmの直方体を斜めに二等分した立体を考えて解き進めても良いでしょう。こちらの解き方の場合は最後に底面が縦1.5cm×横1.5cm、高さが1cmの三角すいの体積を除くことを忘れないようにしてください。

Kの考察

2018年度の第１回入試は大問が９つ、設問は16問で、問題形式、問題数において例年と大差はない年度でした。

合格者平均点は71.1点(受験者平均 51.1点)と芝中学の過去入試の中でも高い点数となりました。問題レベルは16問中 A問題が12問(75%)、B問題が４問(25%)、C問題が０問(０%)で構成されていますので、本年度も、例年通り正答すべきA問題を中心に得点を積み重ねていけた子が合格をつかみ取ったでしょう。

芝中学は１次、２次共に合格者平均点は概ね65点～70点で推移しています。算数で得点を稼ぎたい子は80点以上を狙い、算数が苦手な子は60点は取ることを目標に日々の学習に取り組んでください。

芝中学の過去問題集

芝中学関連情報

芝中学の算数分析｜過去問解説はコチラ