芝中学の算数分析と対策（2021年第1回）

男子難関校の芝中学の算数分析記事です。今回の過去問分析対象は「2021年第１回入試」になります。芝中学の算数の問題構成、傾向と対策方法を知り、合格に向けて是非ご活用ください。

芝中学 2021年入試結果

配点・試験時間

• 国語　100点（50分）
• 算数　100点（50分）
• 社会　75点（40分）
• 理科　75点（40分）

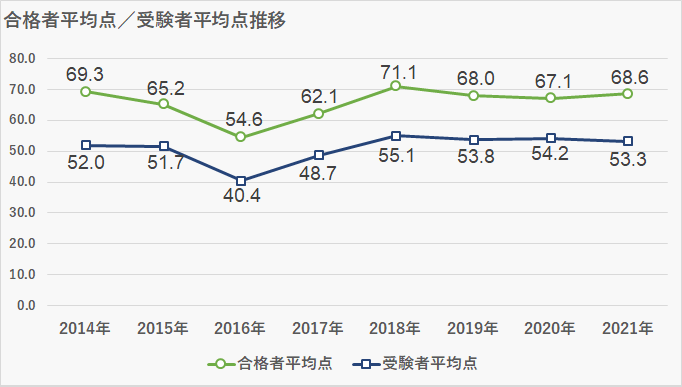
合格者平均点・受験者平均点

• 受験者平均点：53.3点
• 合格者平均点：68.6点

受験者数・合格者数

• 募集者数：150人
• 応募者数：491人
• 受験者数：445人
• 合格者数：187人

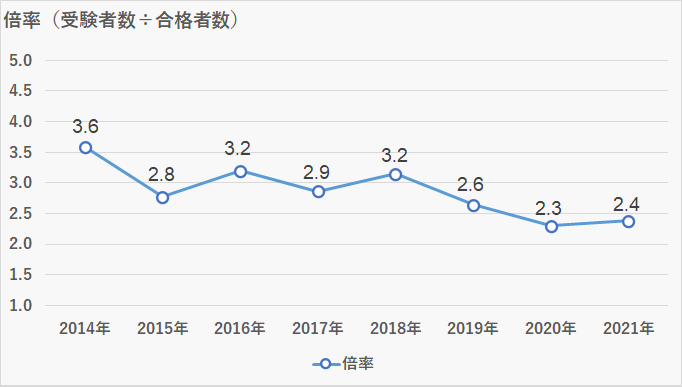
実質倍率

• 倍率：2.4倍

問題別難易度分析

【難易度説明】
A：芝中学合格のために正答したい問題
B：合否を分ける差がつく問題
C：発展問題（間違えても差がつかない）

問題別攻略のポイント

大問１　計算問題

問題数：２
難易度：A，A

(１)　四則演算

例年通り、標準的な計算問題です。10.5や0.25など小数を一発で分数に変換出来ていたか確認しておきましょう。この点も例年通りですね。

(２)　還元算

こちらも標準的な計算問題です。＋－×÷や()など計算ルールに則り、ていねいに計算を進めていきましょう。此方の問題も(１)と同様に、1.875や0.12を一発で分数に変換出来ていたか確認しておきましょう。

また、今回の問題は全て×と÷で繫がった式ですので、はじめから一つ一つ計算するのではなく、全ての分数をまとめて書いて約分するとスピードアップになるでしょう。

大問２　食塩水

問題数：１
難易度：A

３つの食塩水を混ぜる問題です。
15%の食塩水と20%の食塩水の重さが１：２であると分かっているので、先にこの２つを混ぜて、濃度が18\(\large{\frac{1}{3}}\)%の食塩水を作ってから、７% 600gの食塩水と混ぜると答えが出ますね。

あるいは、３つの食塩水を面積図で表し、混ぜ合わせると平均10%になると考えても良いでしょう。

大問３　数の性質

問題数：２
難易度：A，A

約数の個数の典型問題です。必須知識なので、出来なかった生徒は必ずポイントを学びしょう。

(１)の約数の個数が５個の場合は、整数はA⁴（A×A×A×A）の形になります。（※Aは素数）
２番目に小さい整数は、Aが３の時なので、答えは81。

(２)の約数の個数が８個の場合は、整数はA⁷、A³×B、A×B×Cの形になります。
A⁷の１番小さい整数は、Aが２の時の128
A³×Bの１番小さい整数は、Aが２、Bが３の時の24
A×B×Cの１番小さい整数は、Aが２、Bが３、Cが５の時の30　なので、１番小さい整数は24。

大問４　売買損益

問題数：１
難易度：B

原価を①と置いた上で、売った箱数が分かっている「定価」「定価の半額」それぞれの売り上げ及び仕入れ値を出し、その後、売り上げの合計＝仕入れ値の合計となるように、「定価の２割引き」の箱数で調整をする。
標準的な問題ではありますが、上記の方針をスピーディに立てられたか確認しておきましょう。

大問５　平面図形（面積）

問題数：２
難易度：A，A

平面図形の面積比の典型問題。
このような問題でスピーディに正答することで時間を稼ぎたい。

(２)は、３つの辺の比の関係性から、△ABC：△DEFと△DEF：△GHIが同じであることを利用し、
100×\(\large{\frac{19}{50}}\)×\(\large{\frac{19}{50}}\)で求めましょう。

大問６　規則性（数列）

問題数：２
難易度：A，B

(１)は分数の等差数列。論点は、等差数列の和のみなので、確実に点を取りたい問題。実際に問題を解く時も「確実に点を取る問題」であることを強く意識し、個数（62個）や計算が本当に誤っていないか確認した上で答えを求めよう。

(２)は約束記号の問題で、約束記号のルール自体は特に難しい設定は無い。
<A>＝Aとなる、\(\large{\frac{35}{7}}\)までの７個を１周期として考えよう。その後は、周期ごとの和が等差数列となるので、(１)と同様に解き進める。

大問７　規則性

問題数：２
難易度：A，A

大問６に続き、規則性の問題です。
(１)は、最初の玉の個数が分かっているので、規則性を疑いながら、１回目から操作を進めていきましょう。すると、玉の個数が16個となる時が２回（操作１回終了後、操作７回終了後）あるので、操作６回を１周期として答えを求めましょう。

(２)は、４回の操作で玉の個数が０個になったことが分かっています。この問題に限らず、算数は分かっている情報が多い所から解き進めます。今回は、樹形図を用いて最後からさかのぼっていくのが◎。抜け漏れがないように確認しながら進めましょう。

大問８　ニュートン算

問題数：２
難易度：A，B

ニュートン算です。塾のテキストに載っている「はじめの行列が０人になった時」という問題設定ではなく、「はじめの行列とまだ何人か並んでいる行列を比べる」という問題です。解き方に特に違いはありませんが、ニュートン算を本質的に理解している受験生と、形式だけ覚えている受験生は、やや差のついた問題でしょう。

大問９　仕事算（水そうグラフ）

問題数：２
難易度：A，A

複数の蛇口のいるグラフ問題です。まずは「どの蛇口が動いているか」「水そうの半分まで水が入った」「満水になるまで１時間」など問題文の情報をグラフ上に書き入れていきましょう。

(１)は、蛇口Aのみで水そうの半分の水を入れた時間、蛇口AとBで残り半分の水を入れた時間の合計が48分間です。入れた水の体積が同じなので、蛇口Aの１分間で入れる水量を５、蛇口AとBの１分間で入れる水量を11とすると、水を入れるのに掛かった時間の比は逆比の11：５であることが分かります。48分を11：5に分け、33分後が答えです。

(２)は(１)で掛かった時間が分かったので、水そうの容積が５×33×２＝330となります。蛇口Cの１分間で排水する量は11なので、330÷11＝30でサクッと答えが求められますね。

大問10　平面図形（面積）

問題数：３
難易度：A，B，B

最後の問題かつ、2021年度の問題の中では難度高めの問題です。実際の長さ（例：３cm，２mなど）が出ておらず、答えることも「全体の面積の何倍」なので、面積比を考えていきます。

(１)の①の三角形は、パッと「底辺×高さ÷２」の形で面積を出すことが出来ないので、どのように面積比を求めていくか、はじめに方針を立てましょう。

今回は、△AEXから△AFXを引くことで①(△AEF)の面積比を出してみます。※頂点の名前は以下画像の通り
AXはADの\(\large{\frac{1}{4}}\)、△AEXの高さはABの\(\large{\frac{1}{2}}\)なので、□ABCDの面積を１とすると、△AEXは、\(\large{\frac{1}{4}}\)×\(\large{\frac{1}{2}}\)×\(\large{\frac{1}{2}}\)＝\(\large{\frac{1}{16}}\)

△AFXは、AXはADの\(\large{\frac{1}{4}}\)、高さは△AFXと△CFBの相似を利用するとABの\(\large{\frac{1}{5}}\)になります。
よって、△AFXは、\(\large{\frac{1}{4}}\)×\(\large{\frac{1}{5}}\)×\(\large{\frac{1}{2}}\)＝\(\large{\frac{1}{40}}\)

よって、①(△AEF)は、\(\large{\frac{1}{16}}\)－\(\large{\frac{1}{40}}\)＝\(\large{\frac{3}{80}}\)倍になります。

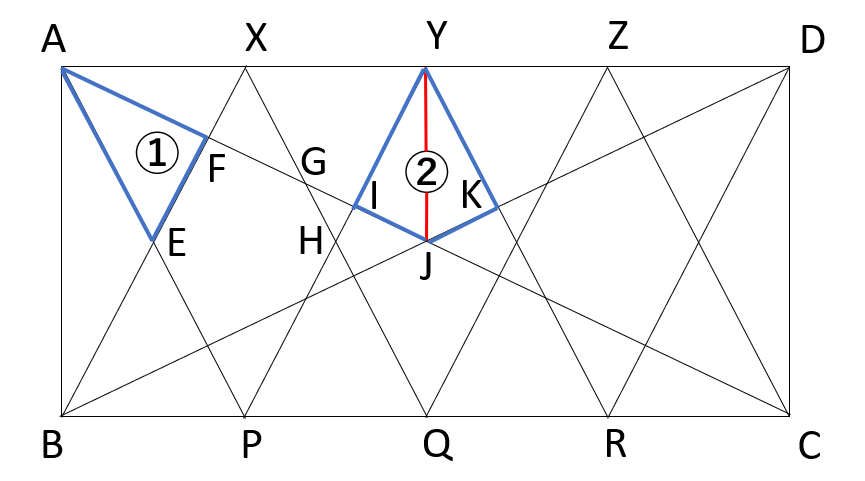
(２)の②の四角形は、①の三角形と同様に、パッと「底辺×高さ」で面積を出すことが出来ないので、どのように面積比を求めていくか、はじめに方針を立てましょう。
例えば、②を△YIJと△YKJに分割し、△AYJと△CQJの相似、△AYIと△CPIの相似を利用すれば、△YIJの面積比を求めることが出来ます。（△AYJ－△AYI＝△YJK）
②の面積は△YIJの２倍なので、２倍して求めましょう。

(３)は、３つの相似な図形（△AEF、△GXF、△GHI）の相似比を求めた後、それぞれの面積比を求めましょう。すると、△AEF、△GXF、△GHI、△YIJの面積比が分かっているので、あとはそれらを足し合わせて４倍すれば斜線部分をすべて合わせた面積比を求めることが出来ます。

Kの考察

2021年度入試は小問数19問で、例年に比べて問題数は多い年でした。その他部分に大きな変化はなく、例年通り、２つの計算問題より始まり、塾の演習で何度か見たことあるような典型題や少し難度の高い問題がバランス良く配置されるという構成になっています。

各問題の難易度分析では、正答したいA問題が14問(74%)、差がつくB問題が５問(26%)、合否に影響のないC問題は０問（０%）となりました。以下は2017年から2021年までの芝中学 第１回入試の問題毎の難度と問題数をまとめたグラフです。2021年入試は問題数は多いものの、その分 難度Aが多く出題され、調整されています。

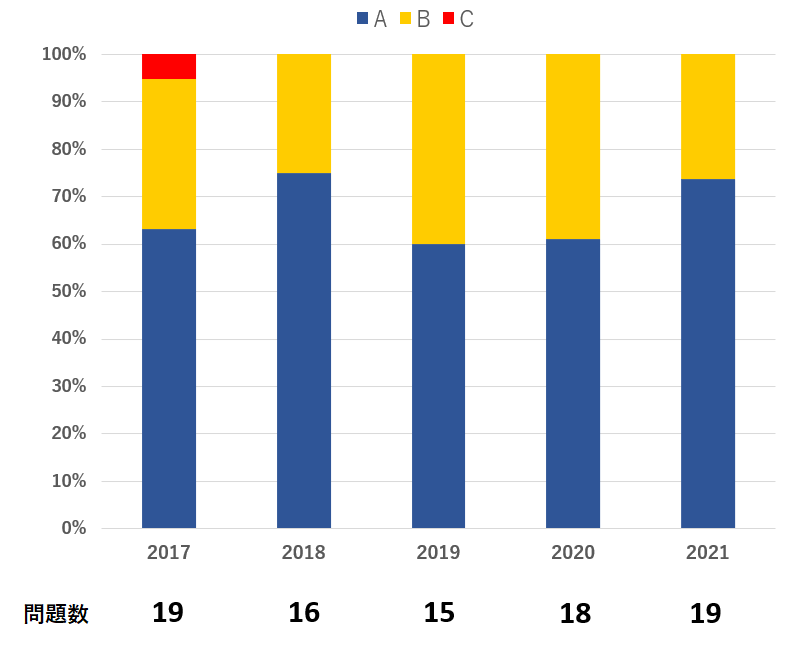
合格者平均点は68.6点。難度Aのみで合格者平均点に達しますが、19問という多数の問題の中であるため、どの問題を解いて得点を取るべきかの判断が出来たかが重要な年度だったと言えます。
合格者平均点を取る目安は、A問題を１～３問落としで11～13問、B問題を５問中１～２問程度という所でしょうか。

50分で小問数19ですので、例年通りではありますが、スピードも求められています。過去問演習では計算問題や典型題などのA問題は正答することを目標とするだけではなく、スピードも意識してください。そのために、日々の自宅学習でも、標準問題や少し難度高めの問題を中心に、１問あたりの時間を把握しながら解き進めることが大事でしょう。

芝中学の過去問題集

芝中学関連情報

芝中学の算数分析／過去問解説はコチラ