ランナーA,B,C,D,E,F,Gの7人が400m競争を行いました。途中経過は次のようでした。
AさんとCさんの間には2人のランナーがいます。
Gさんはこの時点で4位です。
Bさんのすぐ前にEさんがいます。
DさんはBさんの後方にいて,その間には2人のランナーがいます。その後,Aさんが3人を追い抜いてゴールしました。
早稲田中学(2018年)
ゴールしたランナーを1位から順に書きなさい。
男子名門校の早稲田中学より「推理と論証」の問題です。
名探偵になったつもりで各条件から分かる情報をまとめて、答えを求めましょう。推理ですので学年問わずトライしてみてください!
過去問解説記事の使い方は以下をご参照ください。

難度
Lv.2 中学受験 標準問題
全受験生にオススメの中学受験算数の標準問題をまとめています。シンプルな問題設定が多いため、算数の各単元のポイント整理にも有効です。本レベルの演習を通じて、受験算数の基礎固めを行いましょう。
※偏差値の目安やその他難度の詳細などはコチラをご覧ください。
解説
問題文の条件から何が読み取れるのかを考えよう
推理と論証の問題です。問題文の条件から読み取れる情報を用いて、確定している部分とまだ不明な部分を整理しましょう。
そして、不明な部分を推理しながら解き進めていくのが基本的な解き方の流れです。
今回は以下の5つの条件が与えられています。
- AさんとCさんの間には2人のランナー
- Gさんはこの時点で4位
- Bさんのすぐ前はEさん
- Dさんの後方はBさんで,その間には2人のランナー
- その後,Aさんが3人を追い抜いてゴール
①~⑤の条件で、何が確定しているのか、何がまだ不明なのかを1つずつ考え、まとめていきましょう。ただし、入試本番では以下のように文章でまとめている時間はありません。実際に解く際は以下の()の中の内容を問題用紙にメモする程度にしておきましょう。
① AさんとCさんの間には2人のランナー
AとCの間には2人いるが、AとCの順位やどちらが前かは分からない(A,〇,〇,C、C,〇,〇,A)
② Gさんはこの時点で4位
途中経過時点のGは4位(G4位)
③ Bさんのすぐ前にEさん
Bのすぐ前はE(E,B)
④ DさんはBさんの後方にいて,その間には2人のランナー
BはDよりも前にいる。BとDの間には2人いるが、順位は分からない(B,〇,〇,D)
⑤ その後,Aさんが3人を追い抜いてゴール
Aさんは3人を追い抜くことが出来る=Aさんは途中経過の時は4位以下
Aさん以外は誰も追い抜いていない(Aは4位~7位)
整理した情報を組み合わせよう
さて、情報を整理したので組み合わせてみましょう。
- A,〇,〇,CとC,〇,〇,Aのいずれか
- Gは4位
- E,B
- B,〇,〇,D
- Aは4位~7位
③のE,Bと④のB,〇,〇,Dを組み合わせると、途中経過の順位の一部がE,B,〇,〇,Dであることが分かります。
また、Gが4位で確定であることや登場人物は7人しかいないことを考えると、E,B,〇,〇,Dは、以下のようにEが1位か2位に来ないと成り立たないことも分かります。
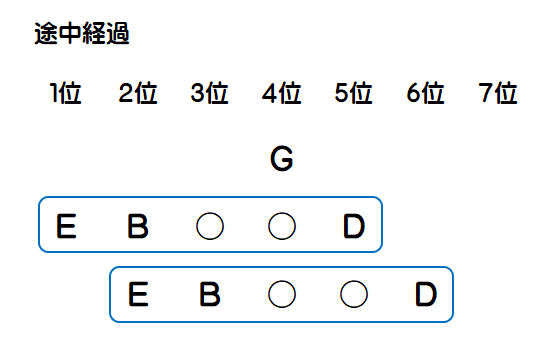
次に、①のA,〇,〇,CとC,〇,〇,Aのいずれかをどこかに入れることを考えると、Eが2位のときはどのようにしてもAとCの間に2人のランナーを入れることが出来ないので、途中経過の時はEが1位であることが分かります。
最後に、⑤のAは4位~7位であることを用い、A,〇,〇,Cではなく、C,〇,〇,Aを3位~6位に入れることが分かります。
よって、途中経過の時は1位からE,B,C,G,D,A,Fの順に並んでいます。答えるべきなのはゴールしたランナーを1位から順にですので、Aに3人追い抜かせて、E,B,A,C,G,D,Fが答えとなります。
 プロ家庭教師K
プロ家庭教師K答えを出す前に、問題文に戻って「何を聞かれているのか」を必ず確認しましょう。答えるものを間違えて失点することのないように!
Kとピヨまるの談話室
 ピヨまる
ピヨまる何だかパズルみたいで楽しかったですね。中学受験の算数では今回のような問題も出るんですか?
 プロ家庭教師K
プロ家庭教師Kそうだね。推理と論証、推理パズル、推理問題など呼ばれ方は様々だけど、今回のような問題も中学受験算数では出題される。最近の入試では思考力を試す学校が増えているので、大問形式で推理と論証が出題されることも珍しくはないかな。その場合は問題文も長いよ。
 ピヨまる
ピヨまるありがとうございます。もし出題されたら、今回のように条件を整理し、「もし、〇〇だったらどうなるかな?」と推理しながら解きます!
 プロ家庭教師K
プロ家庭教師Kなんか今日はまともなコメントだね。
こちらの記事もオススメ☆
・早稲田中学の算数分析/過去問解説はコチラ
・過去問解説記事の一覧はコチラ
・推理と論証の過去問解説はコチラ
・その他の中学受験標準問題(★★☆☆☆)はコチラ

