地点Pと地点Qの間を,A君はPを,B君はQを同時に出発してそれぞれ一定の速さで1往復します。2人が初めてすれ違ったのは,Qから675m離れた地点でした。次にすれ違ったのは,Pから225m離れた地点で,出発してから45分後でした。
(1) 2人が初めてすれ違ったのは,出発してから何分後ですか。
(2) PQ間の距離は何mですか。
海城中学(2021年)
男子難関校の海城中学より「速さ」の問題です。レッツトライ!
過去問解説記事の使い方を読んだ上で、算数の志望校対策や、得点力アップ、弱点補強にご活用ください。

本問題の難度
Lv.2 中学受験 標準問題
全受験生にオススメの中学受験算数の標準問題をまとめています。シンプルな問題設定が多いため、算数の各単元のポイント整理にも有効です。本レベルの演習を通じて、受験算数の基礎固めを行いましょう。
※偏差値の目安やその他難度の詳細などはコチラをご覧ください。
解説
(1) 2人が初めてすれ違ったのは何分後?
まず、状況を整理しましょう。
A君はP、B君はQから同時に出発し、一定の速さで進みます。2人が初めてすれ違う時を状況図に表すと以下の通りとなります。
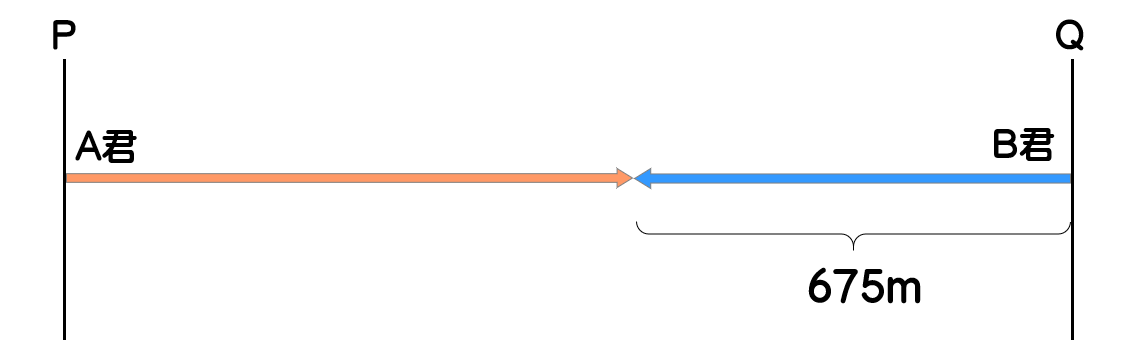
2人が初めてすれ違うのはQから675m離れた地点ですが、B君の速さは分かっていませんので、初めてすれ違うまでの時間を求めることは出来ません。
 ピヨまる
ピヨまるぐぬぬ・・。次だ!次ぃぃ!時を進めよう!
さて、時を進めて、2回目にすれ違う時を状況図に表してみます。A君もB君も折り返して、Pから225m離れた地点ですれ違いますので、以下の通りとなります。(出発してから45分後)

ここで、1回目にすれ違う時と2回目にすれ違う時を比べてみると、1回目にすれ違うまでは、A君・B君の2人でPQ1本分の距離を進んでおり、2回目にすれ違うまでは、A君・B君の2人でPQ3本分の距離を進んでいることが分かります。
A君とB君の速さは一定ですので、掛かる時間の比は、進んだ距離の比と同じく1:3となります。つまり、1回目にすれ違うまでの時間:2回目にすれ違うまでの時間は1:3です。2回目にすれ違う時の時間は出発してから45分後であるため、45÷3=15より、初めてすれ違ったのは、出発してから15分後となります。
(2) PQ間の距離は何m?
(1)で初めてすれ違った時が出発してから15分後と分かりました。この情報とすでに分かっていた情報を結び付けて、何か出来ないか?を考えましょう。
初めてすれ違ったのは、Qから675m離れた地点ですので、B君は15分で675m動いていることが分かります。よって、B君の速さは675÷15=45より、分速45m。
2回目にすれ違ったのは、出発してから45分後なので、45×45=2025より、B君はQから2025m進んでいます。この2025mは状況図の水色の矢印ですので、PQ間の距離は2025-225=1800より、1800mであると分かります。

Kとピヨまるの談話室
 ピヨまる
ピヨまる出発地点が反対側で、同時にスタートし、2人の速さが途中で変わらないというシンプルな条件ならば、1回目にすれ違うまでに掛かる時間と2回目にすれ違うまでに掛かる時間は1:3の関係という事ですね。
 プロ家庭教師K
プロ家庭教師K中学受験の速さではよく問われるポイントの1つだね。単なる暗記ではなく、必ず理屈もセットで押さえておこう。
余裕があれば、3回目、4回目にすれ違うまでに掛かる時間はどうなるか?出発地点が同じときはどうなるか?など派生させて考えてみるのも良い勉強になるよ。
 ピヨまる
ピヨまるほぉ。そうと聞いたら考えない訳にはいかないですね。やったるでぇぇぇぇ!!
こちらの記事もオススメ☆
・海城中学の算数分析/過去問解説はコチラ
・過去問解説記事の一覧はコチラ
・速さの過去問解説はコチラ
・その他の中学受験標準問題(★★☆☆☆)はコチラ

