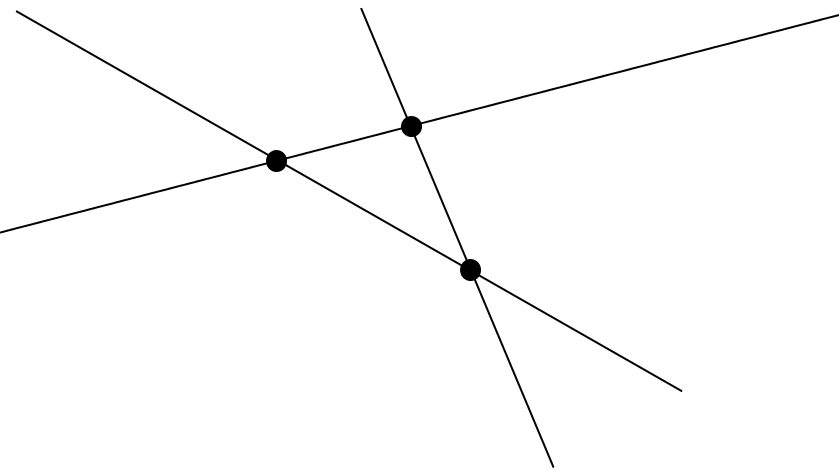
次の□にあてはまる数を求めなさい。
下の図のように、どの２本の直線も必ず交わり、どの３本の直線も同じ点で交わらないように直線をひいていきます。直線を７本ひくとき、交わる点の数は□個です。
攻玉社中学（2022年）
男子難関校の攻玉社中学より「規則性」の問題です。手を動かして試行錯誤しながら、規則を見つける訓練をしてみましょう。過去問解説記事の使い方を読んだ上で、算数の志望校対策や、得点力アップ、弱点補強にご活用ください。
本問題の難度
Lv.２ 中学受験 標準問題
全受験生にオススメの中学受験算数の標準問題をまとめています。シンプルな問題設定が多いため、算数の各単元のポイント整理にも有効です。本レベルの演習を通じて、受験算数の基礎固めを行いましょう。
※偏差値の目安やその他難度の詳細などはコチラをご覧ください。
解説
規則性の問題は「何と何の関係性を聞かれているか」を考えよう！
プロ家庭教師K直線を引いて、交点の個数を求める問題です。
まずは、何本か直線を引いて、交点の個数がどのように増えていくかを考えてみましょう。
ピヨまるすいっ、すいーっ、すいっと。
７本直線引いて、交点が１、２、３，４、…答えは18個です！
プロ家庭教師K…違う！線引きの仕方を間違えているか、交点の個数を数え間違えているね。答えと１個でも違っていたら当然０点なので、しっかり解説を確認して、やり方を修正しましょう。
規則性の問題を解く時には、「何と何の関係性を聞かれているのか」を確認しましょう。「何と何の関係性・・？」とはてなマークが浮かぶかもしれないが、大事なことは問題文に書かれています。
今回は、７本の直線を引いたときの交点の個数を求める問題です。つまり、直線の本数と交点の個数の関係性を聞かれていますね。
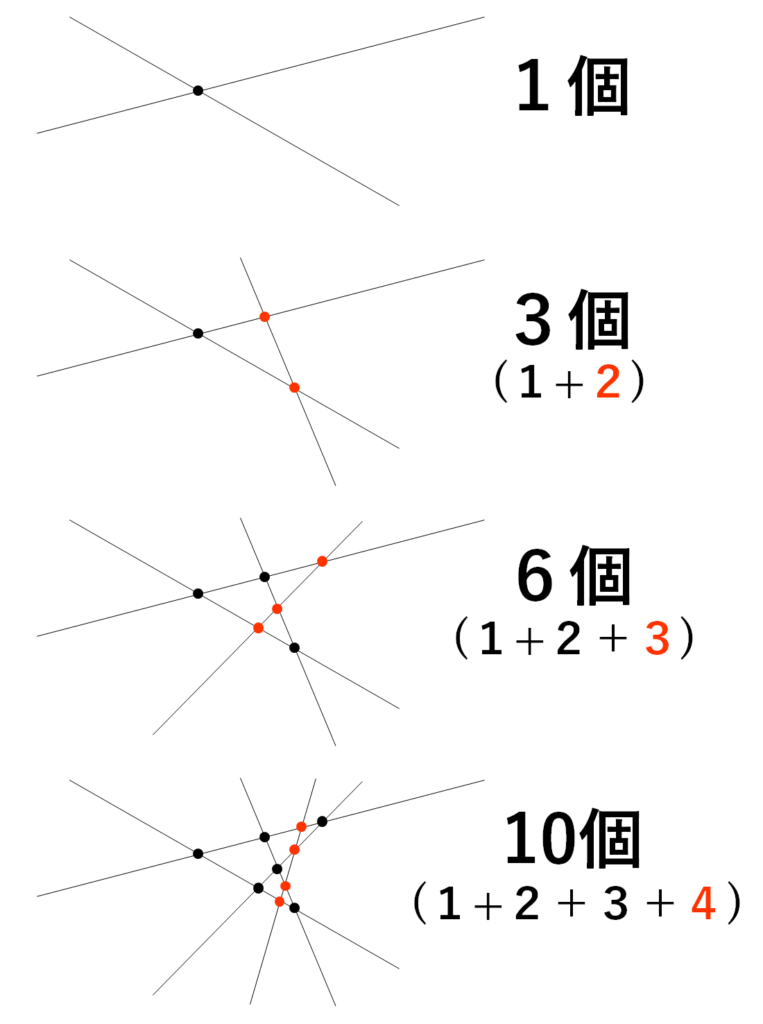
直線の本数と交点の個数の関係性であることが分かったので、実際に直線を１本ずつ引いて、交点の個数がどのように増えていくのかを考えてみましょう。考え終わったら、以下で答え合わせをしてください。
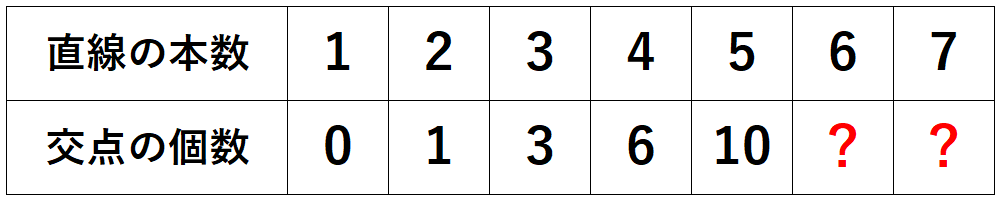
プロ家庭教師K上記の確認結果を表にまとめてみると、以下の通り。何と何の関係性か分かった後は、表にまとめて数列を作り、どのような規則があるのかを確認しましょう。
新たな直線は、すでに引かれている直線とすべて交わるので、直線の数の分、交点の個数が増えることになります。
ピヨまる交点の個数は、
１
３（１＋２）
６（１＋２＋３）
10（１＋２＋３＋４）
となっているので、いわゆる三角数ですね。という事は、直線が７本のときは、１＋２＋３＋４＋５＋６＝21(本)ですか？
プロ家庭教師KOK。今度は正解。
ピヨまる僕は直線７本引いて、18個として間違えましたが、どこが違ったんでしょうか？
プロ家庭教師K７本も線を引いて交点をとると、ぐちゃぐちゃになるから、交点の数え間違いか、そもそも点をつけ忘れているという可能性もあるかな。
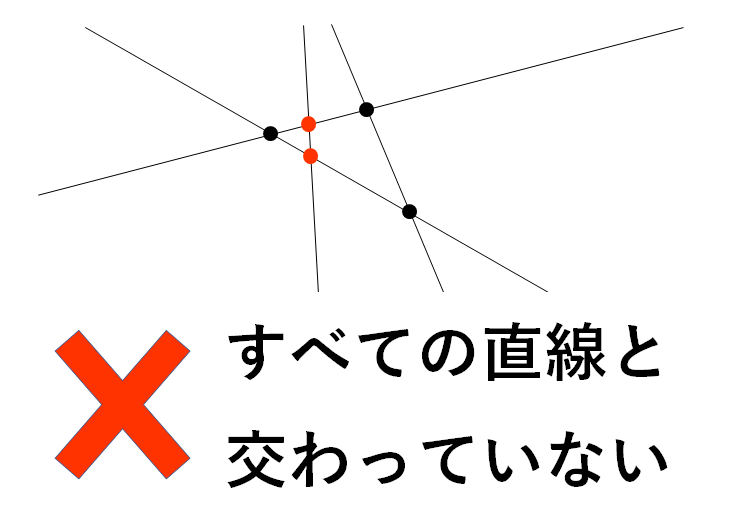
あとは、正しく線を引けているかも確認した方が良いね。次の画像のように、すべての直線と交わっていない直線があるんじゃないか？
- 何と何の関係性を聞かれているのかに着目する。
- 表（数列）を作って、どのような規則かを考える。
Kとピヨまるの談話室
ピヨまる今回は地道に直線を引いて、交点の個数を数えた結果、三角数になっていると発見できたという事だと思いますが、他には交点の個数を出す方法（別解）はないの？
プロ家庭教師K場合の数の発想でも解けるよ。最終的に７本の直線が引かれるが、問題文には「どの２本の直線も必ず交わる」と書かれている。つまり、７本の直線からどの２本を選んだとしても、必ず交わっているということ。
直線のペアの作り方(通り数)＝交点の個数となるので、７本から２本選ぶと考え、交点の個数は\(\large{\frac{７×６}{２×１}}\)＝21(個)と求めることもできる。どちらも理解して使えるようになってほしいかな。
ピヨまる解答がひとつでも、答えが合っていたとしても、色々な解き方に触れてみる。時には、その解き方を理解するのが難しいときもあるだろう。しかし、様々な考え方に触れ、経験することで、算数力を総合的に鍛えることができる。そして、僕をさらなる高みへと連れていってくれるのだ。
プロ家庭教師K良いこと言ってるけど、急にどうした？笑
こちらの記事もオススメ☆
・攻玉社中学の算数分析／過去問解説はコチラ
・過去問解説記事の一覧はコチラ
・規則性の過去問解説はコチラ
・中学受験標準問題（★★☆☆☆）の一覧はコチラ
