次の□にあてはまる数を入れなさい。
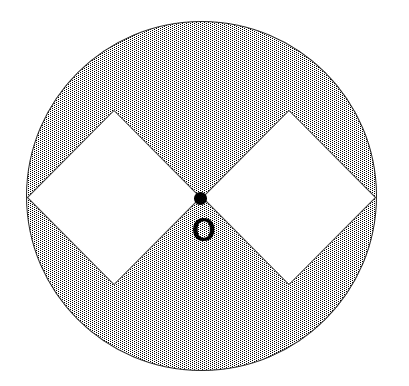
図のように，点Oを中心とする円の中に，１辺の長さが５cmの正方形が２つあります。影をつけた部分の面積は□㎠です。
女子学院中学（2022年）
女子御三家の女子学院中学より「平面図形（面積）」の問題です。円の面積での頻出ポイントのひとつを学ぶことが出来ます。 過去問解説記事の使い方を読んだ上で、算数の志望校対策や、得点力アップ、弱点補強にご活用ください。
本問題の難度
Lv.１ 中学受験 基本問題
各単元の基本問題。１から基本ポイントの確認や弱点補強をしたい受験生や、５～６年生の通常カリキュラムの復習にオススメです。４年生も既習単元の問題は積極的にチャレンジしてみてください。
※偏差値の目安やその他難度の詳細などはコチラをご覧ください。
解説
まずは方針を決めよう！
プロ家庭教師K公式で習っていない図形の面積を求める時は、まずはどのような流れで面積を出すのか、方針を決めよう！
分割、全体から〇〇を引く、等積変形、補助線を引くなどいろいろあるが、今回はどうしようか？
ピヨまるほう。今回はいきなり質問からですか。円の面積から正方形２つの面積を引いて、影の面積を出しますかね。ただ、円の半径が分かっていないので、一工夫する必要がありますよ。
プロ家庭教師Kそこまで分かってりゃ話が早い。あとは解説読んどいて。
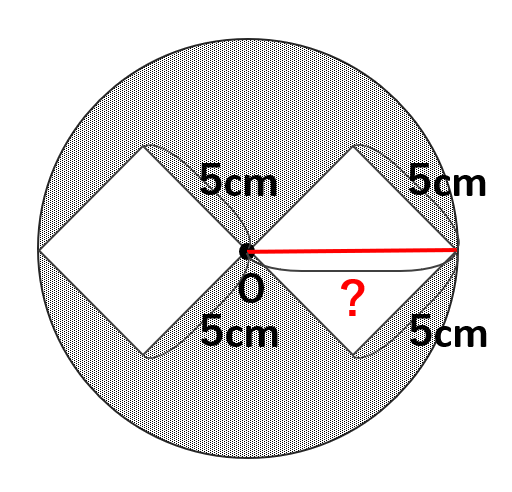
問題文の情報を図に反映すると、上の通り。一辺５cmの正方形２つの面積は、すぐ求めることが出来るでしょう。（５×５×２＝50㎠）
「では、円の面積は？」というと、半径（赤い線）は問題文には書かれていません。今回の問題では、円の半径が正方形の対角線にもなっているので、それを利用して、半径×半径を考えます。
半径（正方形の対角線）をAとすると、正方形の面積はA×A÷２でも求めることが出来ます。また、正方形の面積は25㎠と分かっているので、A×A÷２＝25であり、A×Aは50であると分かります。（つまり、半径×半径は50）
よって、円の面積（50×3.14＝157㎠）から正方形２つの面積を引いて、影の面積は157－50＝107㎠となります。
半径が分からない時は、半径×半径が分からないのかを考える！
Kとピヨまるの談話室
ボブポイントの通り、半径が分からなくても「半径×半径」が分かれば良いってことですね。了解です。はい。
プロ家庭教師Kそうね。今回の問題は、半径は正方形の対角線でもあるから、「半径の長さは分からない」と気付きやすいだろう。
ピヨまる確かに。でも、正方形ってどんな正方形でも形は変わらないので、一辺の長さ：対角線の長さは常に同じな気がするけど、対角線の長さは求めることが出来ないんですか？
プロ家庭教師K君もなかなか鋭くなってきたね。
中学に入って数学を学ぶと求めることができるようになるよ。ちなみに正方形の対角線の長さは一辺の長さの約1.4倍になる。
こちらの記事もオススメ☆
・女子学院の算数分析／過去問解説はコチラ
・過去問解説記事の一覧はコチラ
・平面図形（面積）の過去問解説はコチラ
・その他の中学受験標準問題（★☆☆☆☆）はコチラ
