□にあてはまる数を書き入れなさい。
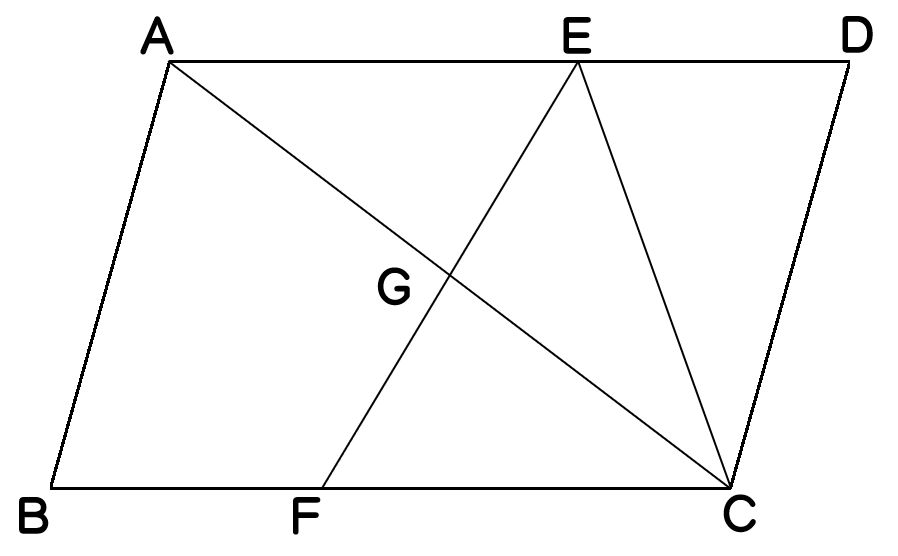
下の図で四角形ABCDは平行四辺形で，AE：ED＝３：２，BF：FC＝３：５です。三角形CEGの面積が15㎠のとき，三角形AGEの面積は□㎠です。
また，台形ABCEの面積は□㎠です。武蔵中学（2016年）
男子御三家の武蔵中学より平面図形（面積）の問題です。相似や面積比をすでに習っている５年生・６年生はぜひトライしてみてください。
過去問解説記事の使い方は以下をご参照ください。
難度
Lv.２ 中学受験 標準問題
全受験生にオススメの中学受験算数の標準問題をまとめています。シンプルな問題設定が多いため、算数の各単元のポイント整理にも有効です。本レベルの演習を通じて、受験算数の基礎固めを行いましょう。
※偏差値の目安やその他難度の詳細などはコチラをご覧ください。
解説
三角形AGEの面積は？
プロ家庭教師K辺の長さの比や面積が出ている部分が出ています。まずは、問題文の情報を図に書き込んでいきましょう。
AE：ED＝３：２、BF：FC＝３：５、三角形CEGの面積が15㎠をそのまま書くと以下のようになります。
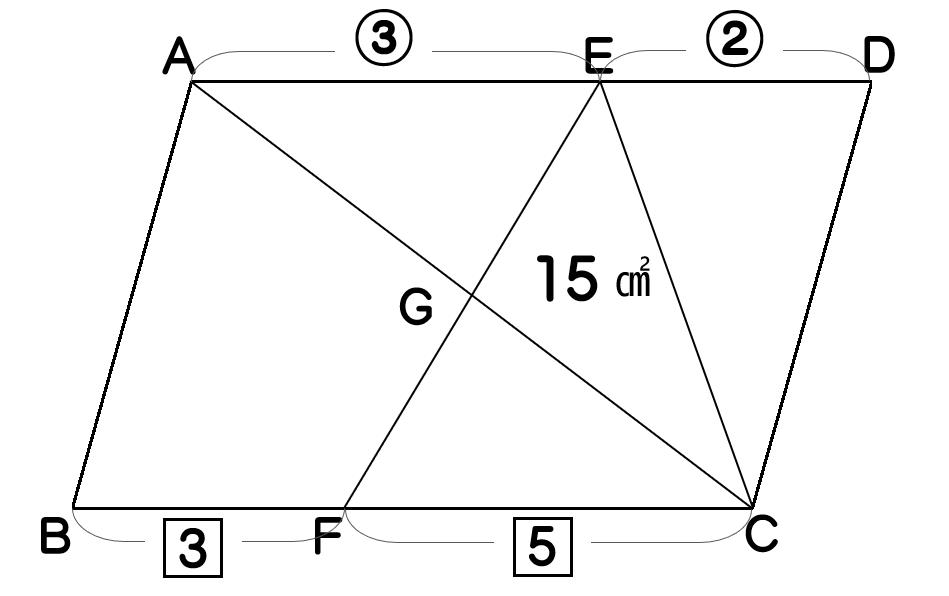
ADとBCは同じ長さなので、比をそろえましょう。⑤＝8⃣であるため、最小公倍数の40にそろえ、AEを24、EDを16、BFを15、FCを25に変えて、最初の作業は完了です。
今回の問題ではじめに聞かれているのは、三角形AGEの面積です。
この図形の中で実際の面積が出ているのは、三角形CEG（15㎠）のみですので、三角形AGEと三角形CEGの関係性を見てみましょう。
プロ家庭教師K聞かれているのは面積比ではなく、実際の面積。そして、実際の面積が分かっているのは三角形CEGのみで、その他に実際の長さの情報も与えられていない。
よって、必ず三角形CEGの面積15㎠の情報を使う。このような視点も持っておきましょう！
三角形AGEと三角形CEGを比べ、それぞれ底辺をAG、GCとしたとき、高さが等しくなることが分かります。高さが等しいので、三角形AGEと三角形CEGの面積比は、底辺のAG：GCと等しくなります。
AG：GCは、三角形AGEと三角形CGFの相似比と同じなので、24：25。
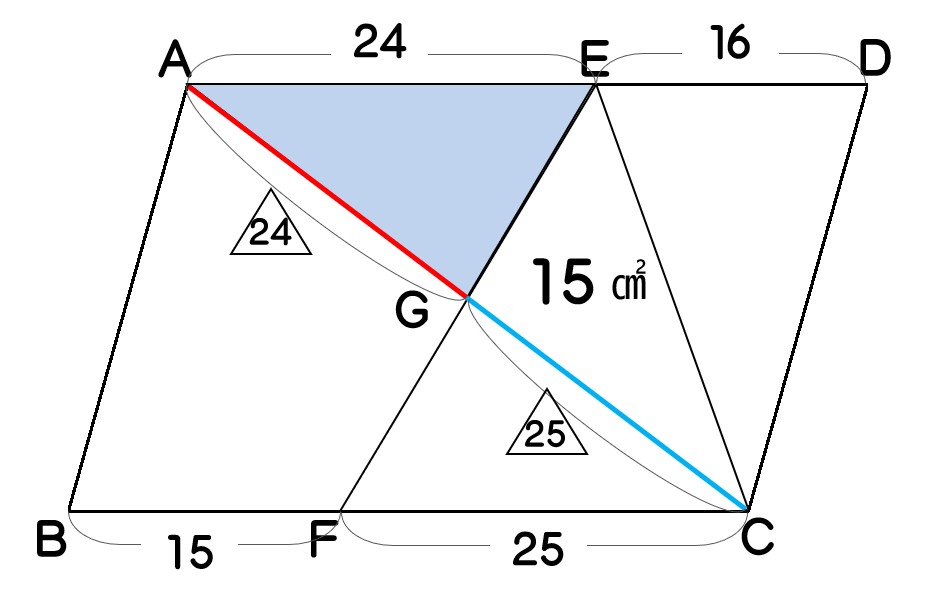
よって、三角形AGEの面積は、15㎠×\(\large{\frac{24}{25}}\)＝14.4㎠です。
台形ABCEの面積は？
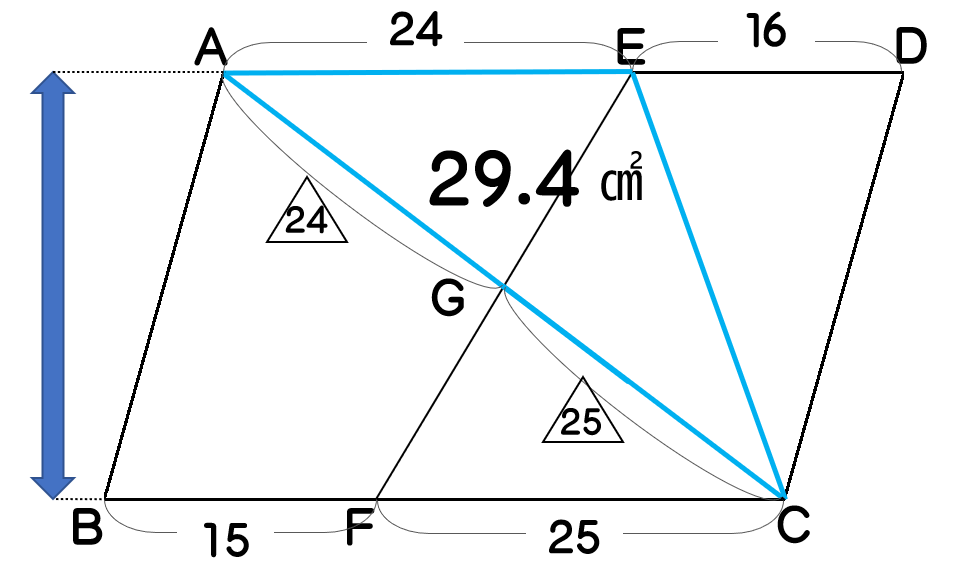
プロ家庭教師K(１)で三角形AGEの面積が14.4㎠と出たので、三角形ACEの面積は15＋14.4＝29.4(㎠)であることが分かります。(２)で聞かれているのは台形ABCEの面積なので、三角形ACEと台形ABCEを比べて、共通部分がないか考えてみましょう。
ピヨまる三角形ACEと台形ABCEは高さが同じですね。
プロ家庭教師Kその通り！今回は三角形と台形ですが、(１)でも使った「高さが等しいとき、底辺の長さの比と面積比が等しい」が使えますね。
三角形ACEの底辺：台形ABCEの上底＋下底は、24：24＋15＋25＝24：64＝３：８になるので、面積比も３：８。よって、台形ABCEの面積は、29.4×\(\large{\frac{８}{３}}\)＝78.4㎠となります。
プロ家庭教師K今回は台形の面積比を一発で求めましたが、台形を三角形ACEと三角形ABCに分割し、三角形ACE：三角形ABC＝24：40＝３：５と面積比を求めて計算しても良いでしょう。
Kとピヨまるの談話室
ピヨまる(１)も(２)もポイントは同じで、「高さが等しいとき、底辺の比が面積の比と同じになる」を使っていましたね。
(２)は三角形と台形で図形が異なりますが、なぜ使えるんでしたっけ？
プロ家庭教師K公式を比べて考えてみよう。以下が三角形と台形の面積の公式です。
・三角形の面積＝底辺×高さ÷２
・台形の面積＝(上底＋下底)×高さ÷２
面積を求める公式の中で「×高さ÷２」は共通しているね。つまり、高さが同じであれば「×高さ÷２」は同じ数になり、面積比には影響を与えないことになる。よって、底辺：上底＋下底がそのまま面積比となる。
言葉で分かりづらければ、実際に数字を当てはめてみて色々と検証してみると良いよ。
こちらの記事もオススメ☆
・武蔵中学の算数分析／過去問解説はコチラ
・過去問解説記事の一覧はコチラ
・平面図形（面積）の過去問解説はコチラ
・中学受験標準問題（★★☆☆☆）の一覧はコチラ
