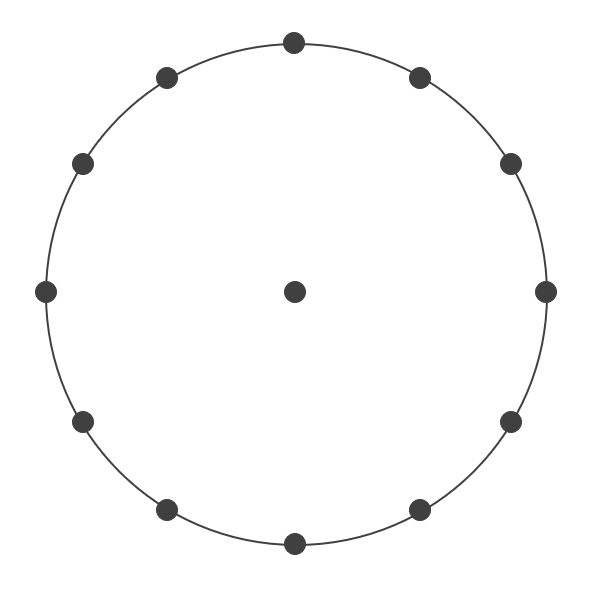
半径３cmの円があります。その円周を12等分する点を打ち、それらの点をつないで正十二角形を作ります。円の面積と正十二角形の面積の差を求めなさい。ただし、円周率は3.14とします。
浦和明の星女子中学（2024年）
女子名門校の浦和明の星女子中学より「平面図形（面積）」の問題です。中学受験では頻出の正十二角形の面積を学ぶことが出来ます。しっかりと確認しておきましょう。
過去問解説記事の使い方を読んだ上で、算数の志望校対策や、得点力アップ、弱点補強にご活用ください！
本問題の難度
Lv.１ 中学受験 基本問題
各単元の基本問題。１から基本ポイントの確認や弱点補強をしたい受験生や、５～６年生の通常カリキュラムの復習にオススメです。４年生も既習単元の問題は積極的にチャレンジしてみてください。
※偏差値の目安やその他難度の詳細などはコチラをご覧ください。
解説
頻出｜正十二角形の面積の求め方！
プロ家庭教師K今回は円の面積と正十二角形の面積の差を問われています。まずはじめに、どの面の面積を出せばいいのかしっかり確認しましょう。
ピヨまる円と正十二角形ではさまれている所が12ヵ所ありますね。すべて同じ大きさで形は何て言うんでしょうか。僕のくちばしの上のような・・。
プロ家庭教師K変な例えは置いといて、今回はそのはさまれた部分の面積を問われているね。
正十二角形の各頂点と円の中心を結ぶと、下の左図の通り、合同な二等辺三角形が12個できますね。今回はこちらを利用して解きます。
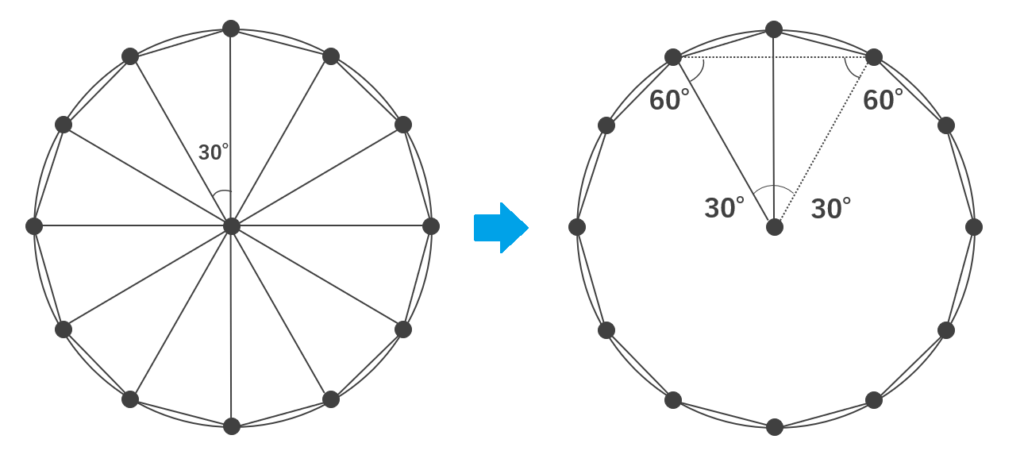
この二等辺三角形は頂角が30°（360°÷12＝30°）なので２つ分で考えてあげると、右の図のように頂角が60°の二等辺三角形、つまり正三角形を作ることができます。
また、この正三角形の１辺は円の半径と同じ３cmなので、それを利用して正十二角形の面積を求めます。
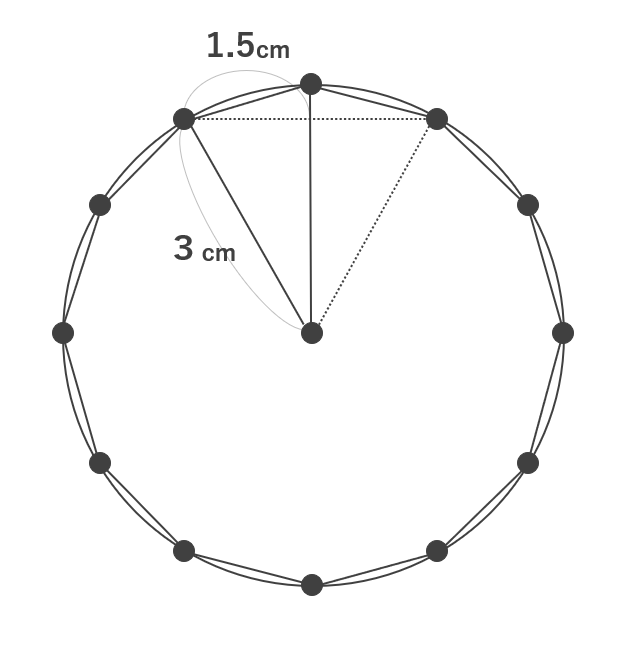
正十二角形を12分割してできる二等辺三角形は底辺が３cm、高さは正三角形の長さの半分1.5cmとなり、面積は３×1.5÷２で求められるので、正十二角形の面積は３×1.5÷２×12＝27㎠となります。（ここで３×1.5÷２＝2.25、2.25×12＝27㎠と計算してしまうと、スピードも遅いし、計算ミスの可能性も高まるので止めましょう！）
円の面積は３×３×3.14＝28.26㎠なので、答えは28.26－27＝1.26㎠となります。
正十二角形の面積は「30°，正三角形」を利用して求めよう！
Kとピヨまるの談話室
ピヨまる正十二角形の問題はちょこちょこ見ますね。塾のテキストでもありました。
ちなみに今回は問題文に書かれた通り、点をつないで正十二角形の辺を作ってから解いてましたが、僕はもう正十二角形マスターなのでこれらを書かずに最初から二等辺三角形のみに着目して解き始めていいですかね？
プロ家庭教師Kうん。問題文を読んでどこを求めるのかを理解した上で、二等辺三角形を描いて解く方法が正しいと確信したならば、それでも良いと思うよ。
ただし、１％でも不安なら辺を書きましょう。12本の線を引くのは数秒で終わるしそれだけでミスや不安要素が取り除けるならば書くべし。
掛かる時間と効果のバランスを考えるといいよ。
ピヨまるなるほど～。確かに入試は基本的にその日一発勝負ですからね。
プロ家庭教師K・・ところで、いつから正十二角形マスターになったんだい？
ピヨまるヒィィ。調子に乗りました！！
こちらの記事もオススメ☆
・浦和明の星女子中学の算数分析／過去問解説はコチラ
・過去問解説記事の一覧はコチラ
・平面図形（面積）の過去問解説はコチラ
・その他の中学受験基本問題（★☆☆☆☆）はコチラ
