6時から7時の1時間で,時計の長針と短針でできる角のうち小さい方の角度が8の倍数となる時刻は何回ありますか。ただし,長針と短針が重なる場合は数えないものとします。
豊島岡女子学園中学(2020年)
女子校最難関の豊島岡女子学園中学より時計算の問題の紹介です。塾の通常テキスト等ではあまり見ない問題ですが、時計算の基本が身についていれば5年生でも問題なく解くことの出来る問題でしょう。ぜひトライしてみてください。
過去問解説記事の使い方は以下をご参照ください。

難度
Lv.2 中学受験 標準問題
全受験生にオススメの中学受験算数の標準問題をまとめています。シンプルな問題設定が多いため、算数の各単元のポイント整理にも有効です。本レベルの演習を通じて、受験算数の基礎固めを行いましょう。
※偏差値の目安やその他難度の詳細などはコチラをご覧ください。
解説
小さい角度が8の倍数になるのは何回?
時計算は、まず基準となる時間の時計を考えましょう。
今回は6時00分の時計を基準にします。6時00分では、長針と短針で出来る角度は、6×30=180°になります。その後、長針は短針よりも速いので、長針が短針に追いつき重なってから、今度は短針に差をつけて7時00分になって終了します。
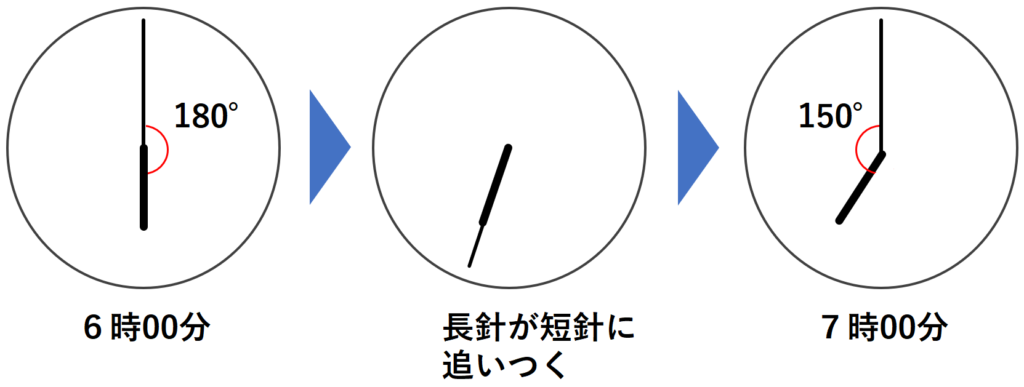
まず、6時00分から長針が短針に重なるまでは、長針と短針で出来る角のうち小さい方の角度は180°~0°です。よって、この間に角度が8の倍数となるのは、180÷8=22…4より、22回であることが分かります。
次に、長針が短針に重なってから7時00分になるまでは、長針と短針で出来る角のうち小さい方の角度は0°~150°です。よって、この間に角度が8の倍数となるのは、150÷8=18…6より、18回であることが分かります。
6時から7時の1時間で、時計の長針と短針で出来る角のうち小さい方の角度が8の倍数となる時刻は22+18=40回です。
Kとピヨまるの談話室
 ピヨまる
ピヨまる考え方は大体合っていたけど、僕は180+150=330、330÷8=41…2で41回にしました。なぜ40回なんですか?
先生、間違ってませんか?!
 プロ家庭教師K
プロ家庭教師K330までに8の倍数が何回あるか?だったら41回でいいけども、今回は長針と短針で出来る角のうち小さい方の角度が8の倍数になる回数だから、短針を境に1回リセットされるんだよね。
以下の画像のように、長針が短針に重なる直前に角度が8°(8の倍数)になってから、次に角度が8°になるまでは長針が短針に16°の差をつけないといけないよね。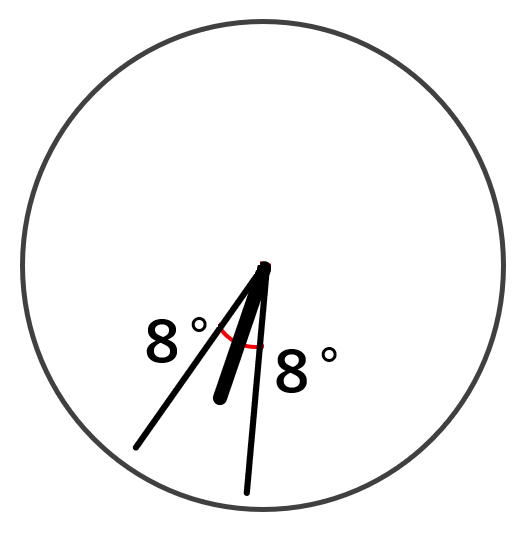
 ピヨまる
ピヨまるふむふむ。そういうことか。
・・・疑って、どうもすみませんでした。
 プロ家庭教師K
プロ家庭教師K声ちっちゃっ!
こちらの記事もオススメ☆
・豊島岡女子学園中学の算数分析/過去問解説はコチラ
・過去問解説記事の一覧はコチラ
・時計算の過去問解説はコチラ
・中学受験標準問題(★★☆☆☆)の一覧はコチラ

