1から6までの数字が書かれた6枚のカードがあります。この中から3枚を取り出して並べ、3桁の数を作ります。次の問いに答えなさい。
(1)3桁の数は、全部で何個作れますか。
海城中学(2020年)
(2)作ることができる3桁の数で50番目に大きい数を答えなさい。
(3)3の倍数である3桁の数は、全部で何個作れますか。
海城中学の頻出単元である「場合の数」のカード問題。2020年一般入試①(2月1日入試)でも出題がありました。内容は典型題ですので、海城中学志望生はもちろんの事、場合の数が頻出している学校を志望する受験生も是非解いてみてください!

難度
Lv.2 中学受験 標準問題
全受験生にオススメの中学受験算数の標準問題をまとめています。シンプルな問題設定が多いため、算数の各単元のポイント整理にも有効です。本レベルの演習を通じて、受験算数の基礎固めを行いましょう。
※偏差値の目安やその他難度の詳細などはコチラをご覧ください。
解説
(1)3桁の数は何個か?
百の位に入る数は1~6のどれでもいいので、6通り
十の位に入る数は百の位に入れた数以外の5通り
一の位に入る数は百の位・十の位に入れた数以外の4通り
よって、6×5×4=120通り
(2)50番目に大きい数は何か?
百の位は1~6まであり、全体の通り数は120通りなので、
百の位が1は20通り、2は20通り、…、6は20通りとなります。(1×5×4=20でもOK)
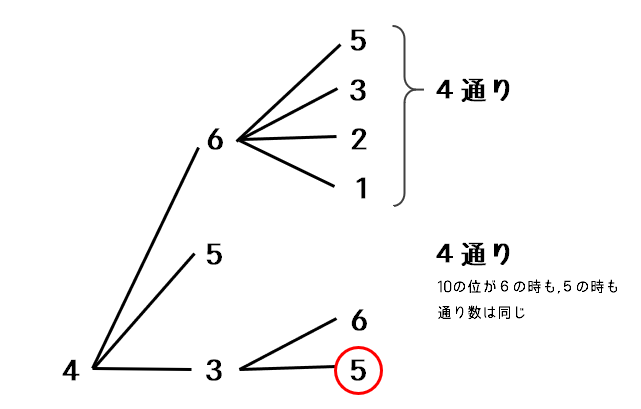
50÷20=2…10より、50番目に大きい数は「百の位が4、かつ、その中で10番目に大きい数」と分かります。百の位が4の時の樹形図を書いてみると、46□の場合が4通り。同様に、45□の場合も4通り。
10番目に大きい数までは残り2つですので、435が答えとなります。
(3)3の倍数である3桁の数は何個か?
3の倍数の判定法は言えますでしょうか?
3の倍数は「各位の数の和が3の倍数となる数」です。
3の倍数の他にも、4の倍数、8の倍数、9の倍数、11の倍数などで倍数判定法があります。パッと言えない受験生はこの機会に併せて確認しておこう!
和が3の倍数となるのは、
(1,2,3)
(1,2,6)
(1,3,5)
(1,5,6)
(2,3,4)
(2,4,6)
(3,4,5)
(4,5,6)の8パターン
百の位、十の位、一の位の順序も考える必要があるので、8×(3×2×1)=48個が答えとなります。
Kとピヨまるの談話室
 ピヨまる
ピヨまる(3)のような数え上げていく問題でのポイントは何かありますか?
 プロ家庭教師K
プロ家庭教師K数え上げの問題で最も怖いことは「数えモレ」だね。
数え上げる際は、極端な数から始めて1つずつズラすということをルールのもと、書き出していこう。今回は最小の(1,2,3)から始めて、1つずつズラしている。
 ピヨまる
ピヨまるふむふむ。確かに1番はじっこから始めて、1つずつ拾い上げればすべてのパターンを数え上げられますね。あざます。
こちらの記事もオススメ☆
・海城中学の算数分析/過去問解説はコチラ
・過去問解説記事の一覧はコチラ
・場合の数の過去問解説はコチラ
・その他の中学受験標準問題(★★☆☆☆)はコチラ

