1,30,275,1468のような同じ数字を2回以上用いないで表される整数を、1から小さい順に並べていきます。このとき、次の問に答えなさい。
(1) 98は何番目ですか。
(2) 987は何番目ですか。
(3) 2018は何番目ですか。
ラ・サール中学(2018年)
男子名門校のラ・サール中学より「場合の数」の問題です。レッツトライ!
場合の数は同校の頻出単元の1つなので、志望者はしっかりと対策をして入試に臨みましょう。
過去問解説記事の使い方は以下をご参照ください。

難度
Lv.3 中学受験 難関校標準問題
中学受験 難関校の標準問題。難関校合格のために必要な標準問題を確実に正答する力をつけたい受験生や、合否を分ける問題を1問でも多く正答できるように得点力をアップさせたい中堅校志望の受験生にオススメ。
※偏差値の目安やその他難度の詳細などはコチラをご覧ください。
解説
(1) 98は何番目か?
 プロ家庭教師K
プロ家庭教師Kこの手の問題の解法としてまず押さえてほしいことは、ケタごとに場合分けして考えるという発想です。今回も場合分けして考えてみます。
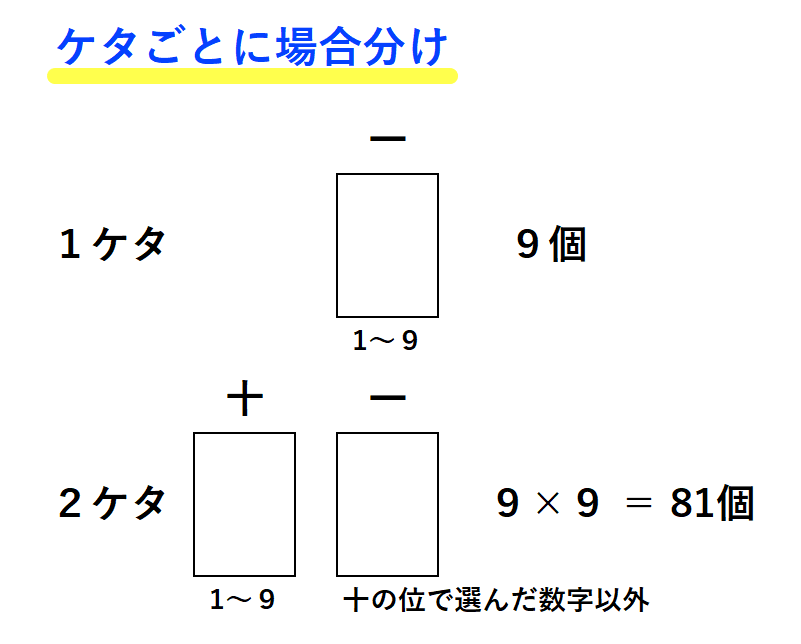
まず、1ケタの場合は特に何も制限が無いので1~9の9個になります。
次に、2ケタの場合を考えます。2ケタの場合は同じ数字を使わないという制限があります。
十の位は、先頭に0が入らないので1~9の9通り。一の位は、0~9の内、十の位で選んだ数字以外であればOKなので、こちらも9通り。よって、2ケタの整数は9×9=81個あります。
98は2ケタの整数の中で最も大きくなるので、9+81=90番目が答えになります。
※99は同じ数字を使っているので不可
(2) 987は何番目か?
 プロ家庭教師K
プロ家庭教師K987は3ケタの整数の中で最も大きい整数です。(1)で1ケタの整数の個数,2ケタの整数の個数を求めているので、(2)は3ケタの整数の個数のみ考えましょう。
3ケタの場合、百の位は1~9の9通り、十の位は百の位で選んだ数字以外の9通り、一の位は百の位・十の位で選んだ数字以外の8通り。よって、3ケタの整数の個数は、9×9×8=648個あります。
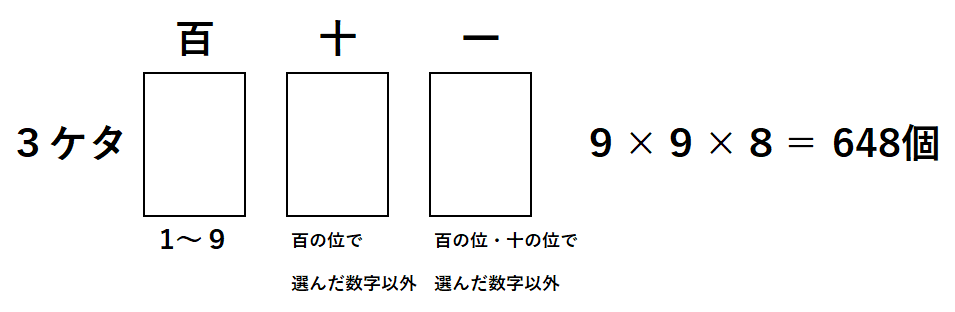
987は3ケタの整数の中で最も大きい整数なので、90+648=738番目になります。
 プロ家庭教師K
プロ家庭教師K考え方が分かっていれば、さくさく解けるね。
(3) 2018は何番目か?
次は2018です。今回は4ケタの整数ですが、(1)(2)と異なる点は4ケタの整数の中で最大ではない点です。
まずは、1□□□(1000台)の整数の個数を求めて、その後に2□□□(2000台)の整数の個数を考えましょう。
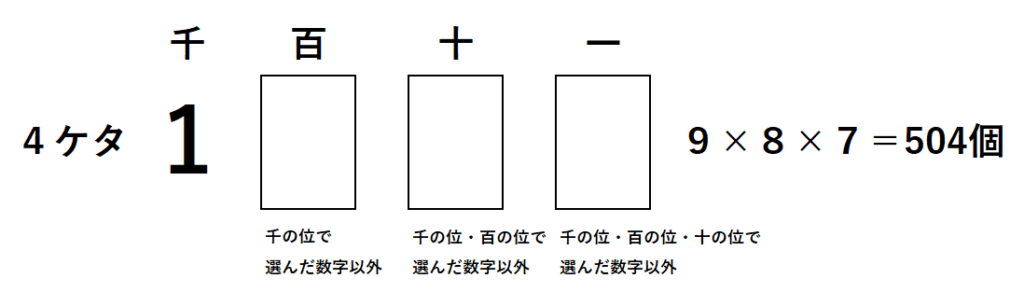
千の位は1で確定。
百の位は0~9の内、1以外の9通り。
十の位は千の位・百の位で選んだ数字以外OKなので、8通り。
一の位は千の位・百の位・十の位で選んだ数字以外OKなので、7通り。
よって、1□□□(1000台)の整数は、9×8×7=504個あります。
 プロ家庭教師K
プロ家庭教師Kここまで来たら、あとは2□□□の形で2018が何番目かを出すだけです。残りの個数も少ないので、確実に正答するために書き出すのをオススメします。
 ピヨまる
ピヨまる同じ数字は使ってはいけないので、2000~2009は全て0を2回使うので、アウトですね。
2010、2011、2012も同じ数字を使っているので、アウトです。
2□□□の形は、2013,2014,2015,2016,2017,2018の6個あります。
よって、2018は、738+504+6=1248番目が答えになります。
Kとピヨまるの談話室
 ピヨまる
ピヨまる僕の野生のヒヨコ勘によると、色々と別解がありそうな気がしますが、どうでしょうか?
 プロ家庭教師K
プロ家庭教師Kその勘は初めて聞いたけど、するどい勘だね。てか野生なの?
例えば、(1)は以下のような別解があるよ。
【別解①】
1ケタ・2ケタをまとめて考えても解くことが出来る。十の位は0~9の10通り、一の位は0~9の内、十の位で選んだ数字以外の9通り。よって、10×9=90番目
【別解②】
1~99は、99個。
この99個の中で同じ数字を使う整数は11,22,・・・,88,99の9個なので、99-9=90番目
 ピヨまる
ピヨまるなるほど。別解①は先頭の十の位に0が入っていますが、良いんですか?
 プロ家庭教師K
プロ家庭教師K十の位に0を入れないと、一番小さい整数が10となってしまい、1~9の1ケタの整数が表せない。
別解は1ケタ・2ケタをまとめて考えているので、十の位を0、一の位を5にした場合は、05となり、それは5を表していることになるよ。

こちらの記事もオススメ☆
・ラ・サール中学の算数分析/過去問解説はコチラ
・過去問解説記事の一覧はコチラ
・場合の数の過去問解説はコチラ
・その他の難関校標準問題(★★★☆☆)はコチラ

