次の□にあてはまる数を答えなさい。
７個の同じおかしをAさん，Bさん，Cさんの３人に分けるとき，その分け方は□通りあります。ただし，必ず１人に最低でも１個のおかしを分けることにします。
栄東中学・A日程（2018年）
１月受験の代表校である栄東中学より「場合の数」の問題です。以下の過去問解説記事の使い方を読み、得点力アップや弱点補強にご活用ください。
本問題の難度
Lv.１ 中学受験 基本問題
各単元の基本問題。１から基本ポイントの確認や弱点補強をしたい受験生や、５～６年生の通常カリキュラムの復習にオススメです。４年生も既習単元の問題は積極的にチャレンジしてみてください。
※偏差値の目安やその他難度の詳細などはコチラをご覧ください。
解説
(１) １つずつずらして数え上げる
プロ家庭教師K３人で７個持つので、A＋B＋C＝７という式になります。和の７をA，B，Cの３人にどのように分解するかを考える「和分解」と考えられます。
まず、A，B，Cの３人は最低でも１個のおかしをもらえるので、確定している３個は取り除きます。
７ー３＝４。この４個を３人にどのように分けるかを考えていきましょう。
４個のおかしを３つに分ける方法は以下の４パターンがあります。数えモレがないように、極端な数から始めて、１つずつズラしていきましょう。
（４，０，０）
（３，１，０）
（２，２，０）
（２，１，１）
次に、３つに分けたおかしを誰に配るかを考えます。
（４，０，０）や（２，２，０）（２，１，１）のような（〇，●，●）のパターンは、〇を誰に配るかで通り数が決まるので、（〇，●，●）（●，〇，●）（●，●，〇）の３通りです。
（３，１，０）のような（〇，●，△）のパターンは、３個もらうのはAさん，Bさん，Cさんの３通り、１個もらうのは残り２人の２通り、…と考え、配り方は３×２×１＝６通りとなります。
（４，０，０） ３通り
（３，１，０） ６通り
（２，２，０） ３通り
（２，１，１） ３通り
よって、３＋６＋３＋３＝15通りが答えです。
プロ家庭教師K（４，０，０）
（０，４，０）
（０，０，４）
（３，１，０）
（３，０，１）
・
・
などのようにすべての通り数を書くのは止めましょう！
Kとピヨまるの談話室
ピヨまるこの問題、僕も解説通りのやり方で解きました。
ただ、塾の先生が違う解き方を説明していたんですよね。何だっけな？力士とか言ってた気がします。
プロ家庭教師Kどすこい！どすこい！
力士ではなく仕切りだと思うぞ。塾の上位クラスでは通常の解き方に加えて、仕切りを使った解き方を説明されることがある。さては、上位クラスだな？！
ピヨまるあ？バレました？上位ですよ。
なんか自慢みたいになっちゃったなぁ。
プロ家庭教師Kという事で、別解いきます！！
(１)別解 仕切りを使って考えてみよう！
７個を３人に分ける仕切りを考える
プロ家庭教師K７個の同じおかしを３人にどのように分けるかなので、２つの仕切りを使って考えることもできます。
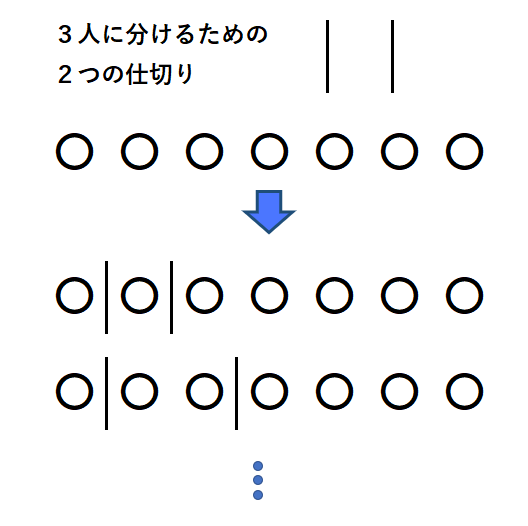
上の画像の↓以降の仕切りでの分け方は、
１つ目は、Aさんにおかし１個、Bさんにおかし１個、Cさんにおかし５個
２つ目は、Aさんにおかし１個、Bさんにおかし２個、Cさんにおかし４個 を表しています。
仕切りを入れる場所は？
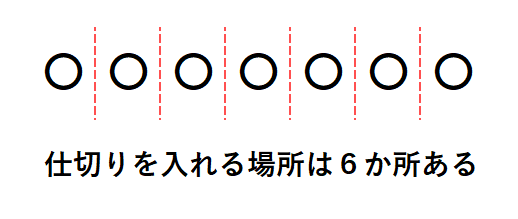
それぞれの人が必ず１個以上のおかしを持つように仕切りを入れるので、仕切りを入れる場所は６か所あります。２つの仕切りの入れ方は、この６か所から２か所の選び方を考えればよいので、\(\large{\frac{６×５}{２×１}}\)＝15より、15通りが答えです。
こちらの記事もオススメ☆
・栄東中学の算数分析／過去問解説はコチラ
・過去問解説記事の一覧はコチラ
・場合の数の過去問解説はコチラ
・その他の中学受験基本問題（★☆☆☆☆）はコチラ
