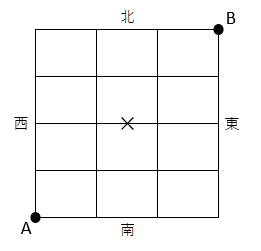
右の図のように,東西方向に5本,南北方向に4本の道があります。これらの道を通って,遠回りしないでA地点からB地点へ行きます。このとき,×印のついた道を通らない行き方は何通りあるかを求めなさい。
東邦大学付属東邦中学(2015年)
千葉県の人気中高一貫校の東邦大学付属東邦中学より「場合の数」の道順問題です。レッツトライ!
過去問解説記事の使い方は以下をご参照ください。

問題の難度
Lv.1 中学受験 基本問題
各単元の基本問題。1から基本ポイントの確認や弱点補強をしたい受験生や、5~6年生の通常カリキュラムの復習にオススメです。4年生も既習単元の問題は積極的にチャレンジしてみてください。
※偏差値の目安やその他難度の詳細などはコチラをご覧ください。
解説
道順問題の解き方
道順問題の基本的な解き方は1マスずつていねいに通り数を書き進めていくことですね。
まずは、北方向に1を4回、東方向に1を3回書く所から始めましょう。
スタートのA地点を(北0東0)、ゴールのB地点を(北4東3)と表すことにすると、今回は(北2東1)から(北2東2)に進む道が通ることが出来なくなっています。
 プロ家庭教師K
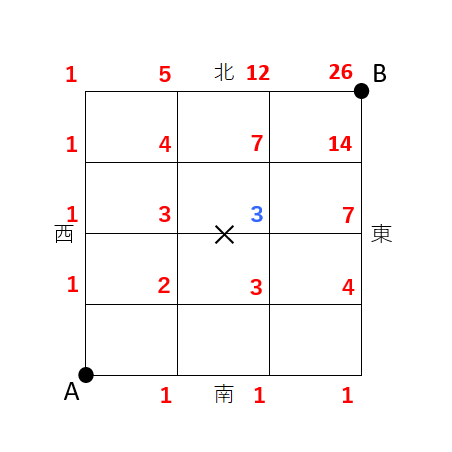
プロ家庭教師K北2,東2の通り数を3+3=6通りにしないように気を付けましょう。
※以下画像の青字の部分です。
気を付ける部分としてはその点のみですね。道順問題の基本的な問題ですので、受験生は必ず正答して、点を稼いでおきたい問題です。
解説(別解)-道順の公式を使おう!-
道順の問題は、場合の数のコンビネーションを利用して解くことが出来ますので、今回はコンビネーションを利用した解き方を別解で載せておきます。
なお、別解は「×印の道を通らない行き方=全体の通り数-×印の道を通る通り数」と考えて、解き進めていきます。
別解
×印の道も通ることが出来るとすると、A地点からB地点までは、必ず縦に4本、横に3本、計7本の辺を進みます。コンビネーションの考えと同様に、7本の内、横3本をいつ進むのかを確定させれば、AからBまでの行き方を求めることが出来ます。
よって、7つから3つ選ぶと同様に\(\large{\frac{7×6×5}{3×2×1}}\) = 35通り
次に、AからBまで行くときに必ず×印の道を通ることを考えます。
×印の道の左端をC地点、右端をD地点とすると、A地点からC地点までは縦に1本、横に2本で計3本進みますので、進み方は\(\large{\frac{3}{1}}\) = 3通り
D地点からゴールのB地点までも同様ですので、3通りとなります。
Aから×印の道を通り、Bまで行く時の通り数は、3×1×3=9通りです。
全体の通り数である35通りから9通りを引き、×印の道を通らない行き方は26通りであることが分かります。
Kとピヨまるの談話室
 ピヨまる
ピヨまる道順問題はコンビネーションでも解けるんですね。中々便利そうで、僕好みですよ。でもこの解き方って常に使えるんでしょうか?
 プロ家庭教師K
プロ家庭教師K今回のように問題設定が簡単な場合は、コンビネーションを用いた方が時短になることは多いね。でも条件がもっと複雑な問題は、1マスずつていねいに書き進めていく方がいいかな。調子に乗ってコンビネーションを活用しようとして、間違えたら意味ないからね。
また、今回は詳しくは載せていないけど、コンビネーションを利用する上で重要なことは、道順問題がなぜコンビネーションで解けるのか?という理由・背景を正しく理解すること。
少しでも不安なら、手を動かして、1マスずつ通り数を埋めていこう!
 ピヨまる
ピヨまる手を動かすことが大事なんですね。よーし、動かすぞぉ。ドリャアアア、アチョーーーー、シュタタタタタタ!
 プロ家庭教師K
プロ家庭教師Kいや、そういう事じゃないんだよなぁ。
こちらの記事もオススメ☆
・東邦大学付属東邦中学の算数分析/過去問解説はコチラ
・過去問解説記事の一覧はコチラ
・場合の数の過去問解説はコチラ
・その他の中学受験基本問題(★☆☆☆☆)はコチラ