次の問いについて□にあてはまるものを入れなさい。
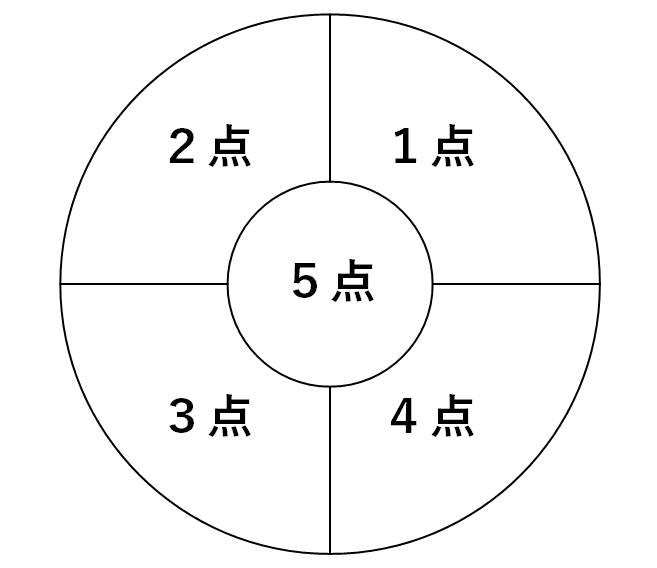
図のような的に矢を3回射って,そのうち高い2回の点数の平均を最終得点とするゲームがあります。J子,G子,K子がこのゲームをしたところ,次のようになりました。
・的を外した人はいませんでした。
・3回のうち2回以上同じ点数を取った人はいませんでした。
・K子の1回目の点数は1点でした。
・3人それぞれの最も低い点数は,すべて異なっていました。
・最終得点は,J子の方がG子よりも1点高くなりました。
・3人の最終得点の平均は4点でした。
J子の最終得点は□点,K子の3回の点数は低い方から順に1点,□点,□点でした。
女子学院中学(2022年)
女子御三家の女子学院中学より「推理と論証」の問題です。条件が多い問題ですので、ていねいに整理をして答えを出すという情報処理能力を問われていますね。 過去問解説記事の使い方を読んだ上で、算数の志望校対策や、得点力アップ、弱点補強にご活用ください。

本問題の難度
Lv.2 中学受験 標準問題
全受験生にオススメの中学受験算数の標準問題をまとめています。シンプルな問題設定が多いため、算数の各単元のポイント整理にも有効です。本レベルの演習を通じて、受験算数の基礎固めを行いましょう。
※偏差値の目安やその他難度の詳細などはコチラをご覧ください。
解説
J子の最終得点とK子の3回の点数は?
登場人物が3人いて、さらに複数の条件があるので、まずは一つ一つ整理していきましょう。
条件1:的を外した人はいませんでした。
→3人とも1回も0点を取っていない。
条件2:3回のうち2回以上同じ点数を取った人はいませんでした。
→3人とも3回の点数は違う点数だった。最終得点として最も高い得点は4点と5点の平均である4.5点となる。(5点を2回取ることはできない)
条件3:K子の1回目の点数は1点でした。
→K子は1回目は1点で、2回目・3回目は1点ではない。
条件4:3人それぞれの最も低い点数は,すべて異なっていました。
→K子の最も低い点数は1点であるため、J子、G子の最も低い点数の組み合わせは(2点,3点)(3点,2点)のいずれか。
条件5:最終得点は,J子の方がG子よりも1点高くなりました。
→J子の最終得点(2回の点数の平均)は、G子の最終得点よりも1点高い。
条件6:3人の最終得点の平均は4点でした。
→3人の最終得点の平均は4点。条件2で判明した最終得点としての最高が4.5点であることも考えると、3人の最終得点の組み合わせは(4.5点,4.5点,3点)(4.5点,4点,3.5点)のいずれかだが、(4.5点,4.5点,3点)は条件5に当てはまらないので、不可。
3人の最終得点は(4.5点,4点,3.5点)と確定し、最終得点はJ子:4.5点、G子:3.5点、K子:4点であることも確定する。
 プロ家庭教師K
プロ家庭教師K文字だけだと分かりづらいので、表で情報を整理してみますか。
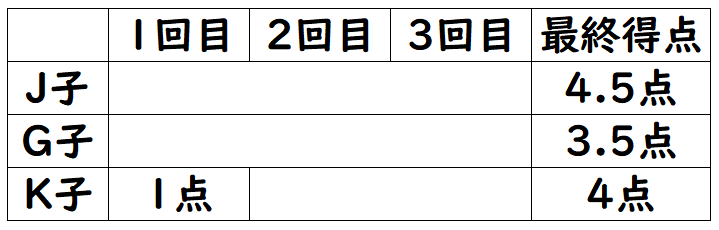
J子、G子、K子の最終得点から考えると、最終得点が4.5点になる点数の組み合わせは(4点,5点)、3.5点になる組み合わせは(2点,5点)(3点,4点)、4点になる組み合わせは(3点,5点)となります。
G子は最終得点のみ考えると(2点,5点)と(3点,4点)の2パターンがあり得ますが、最終得点は高い2回の点数の平均なので、(2点,5点)の場合は残りの1回は1点になります。すると、最も低い点数が1点になる人がG子とK子の2人になってしまい、「条件4:3人それぞれの最も低い点数は,すべて異なっていました。」に当てはまりません。
よって、表は以下の通りに更新できます。
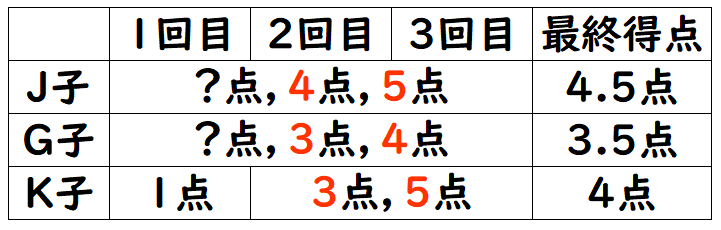
残りのJ子とG子の点数は、「条件4:3人それぞれの最も低い点数は,すべて異なっていました。」を考えると、J子が3点、G子が2点に確定するので、最終的な表は以下の通りになります。
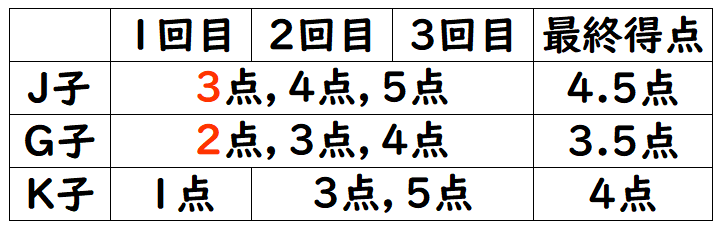
よって、J子の最終得点は4.5点。K子の3回の点数は低い方から順に1点,3点,5点となる。
 プロ家庭教師K
プロ家庭教師KK子の3回の点数は低い方から順に1点,□点,□点と書かれているので、5点・3点の順で書いている子は残念ながら×です。
Kとピヨまるの談話室
 ボブ
ボブ推理と論証はやっぱりパズルみたいで好きですね。何か勉強って感じがしないです。
 プロ家庭教師K
プロ家庭教師K推理と論証はさまざまな条件が与えられるけど、個々の条件だけを見るのではなく、条件Aと条件Bを組み合わせて何が言えるか?などを考えると、道筋が見えてくると思うよ。名探偵になったつもりで考えながら進めよう。
 ボブ
ボブ名探偵…。そういえば、某漫画の「見た目は子供、頭脳は大人」とはまさに僕にふさわしい言葉だと思いますよ。「犯人は…この中にいる!!!」と人生の内で1回ぐらい言ってみたいです。
 プロ家庭教師K
プロ家庭教師K明日、勝手に夕食つまみ食いしてから、言ってみれば?
こちらの記事もオススメ☆
・女子学院中学の算数分析/過去問解説はコチラ
・過去問解説記事の一覧はコチラ
・推理と論証の過去問解説はコチラ
・その他の中学受験標準問題(★★☆☆☆)はコチラ