11で割ると7余り,31で割ると11余る整数の中で,1950にもっとも近い整数はいくつになりますか。
豊島岡女子学園中学(2019年)
豊島岡女子学園中学より、数の性質の問題です。豊島岡以外のどの学校でも出題される可能性のある頻出問題ですので、正確に、かつスピーディーに解けるか確認しておきましょう!

難度
Lv.2 中学受験 標準問題
全受験生にオススメの中学受験算数の標準問題をまとめています。シンプルな問題設定が多いため、算数の各単元のポイント整理にも有効です。本レベルの演習を通じて、受験算数の基礎固めを行いましょう。
※偏差値の目安やその他難度の詳細などはコチラをご覧ください。
解説
11で割ると7余り,31で割ると11余る整数の1つ目は?
商と余りの問題ですね。どの塾に通っていても以下のような問題を解いた記憶があると思います。
「4で割ると1余り、5で割ると3余る整数の中で最も小さい整数はいくつですか?」
「5で割ると2余り、6で割ると3余る整数のうち、100に最も近い整数はいくつですか?」などなど。
 プロ家庭教師K
プロ家庭教師K商と余りは、以下のどの出題パターンなのかを判断しましょう。
- 「余り」が同じパターン
- 「差」が同じパターン
- 「それ以外」のパターン
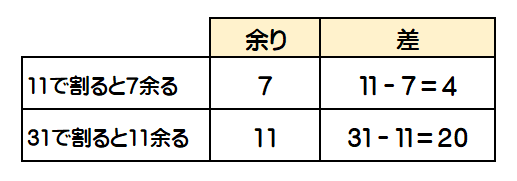
今回は「11で割ると7余り,31で割ると11余る整数」ですので、以下の表のように、余りと差はどちらも異なっています。
よって、③の「それ以外」のパターンで解き進めていくこととなります。
それ以外のパターンのときは、条件にあてはまる整数の1個目を地道に見つけ出します。
キーワードは「1個目地道!」
探し方は色々とありますが、今回は「11で割ると7余る整数」「31で割ると11余る整数」をそれぞれ書き出してみて、同じ整数を見つけてみましょう。

以上より、「11で割ると7余り,31で割ると11余る整数の1個目」は73であることが分かりますね。
 プロ家庭教師K
プロ家庭教師K今回は「11で割ると7余る整数」「31で割ると11余る整数」をそれぞれ書いて探しましたが、探し方はその他にも色々とあります。
例えば、割る数が大きい「31で割ると11余る整数」を11,42,73,104,135,…と初めに書き出してから、その整数が11で割ると7余るのかを計算して確かめていきます。すると、73が73÷11=6…7で当てはまることが分かります。
条件に当てはまり、1950に最も近い整数は?
さて、本問題は1個目を答えるのではなく、1950に最も近い整数を答える必要がありますね。次はそちらを考えてみましょう!
11で割ると7余り,31で割ると11余る整数の1個目は73であり、2個目以降は11と31の最小公倍数である341ずつ増えていきます。よって、73+341×●の計算結果が1950に最も近い整数となるときが答えであることが分かります。
1950-73=1877
1877÷341=5…172 なので、
●=5のときと●=6のときを考えます。
73+341×5=1778(1950との差は172)
73+341×6=2119(1950との差は169)
※差172は341÷2=170.5より大きいので●=5のときは答えではないと考えることもできます。
2119の方が1950との差が小さいので、2119が答えとなります。
今回、聞かれているのは「1950に最も近い整数」。
答えは1950より大きくても問題ないが、焦って、答えは1950以下として勘違いしてしまうのがよくあるミスパターン。商と余りが出題されたら、必ず確認する項目として頭の片隅に入れておこう。
Kとピヨまるの談話室
 プロ家庭教師K
プロ家庭教師K今回は商と余りの入試問題でした。
どの塾に通っていても、何度も取り組むことになる典型題の1つだね。余りも差も等しくない場合の解き方を忘れてしまっていた子は「次回出題されたら、自分はどの部分を確認して、どう解き進めていけば正答できるのか?」という視点で解説を熟読してみてください
 ピヨまる
ピヨまる努力家の僕は、余りが同じパターン、差が同じパターンがどんな問題なのかも同時に確認しておきます!
こちらの記事もオススメ☆
・豊島岡女子の算数分析/過去問解説はコチラ
・過去問解説記事の一覧はコチラ
・数の性質の過去問解説はコチラ
・その他の中学受験標準問題(★★☆☆☆)はコチラ

