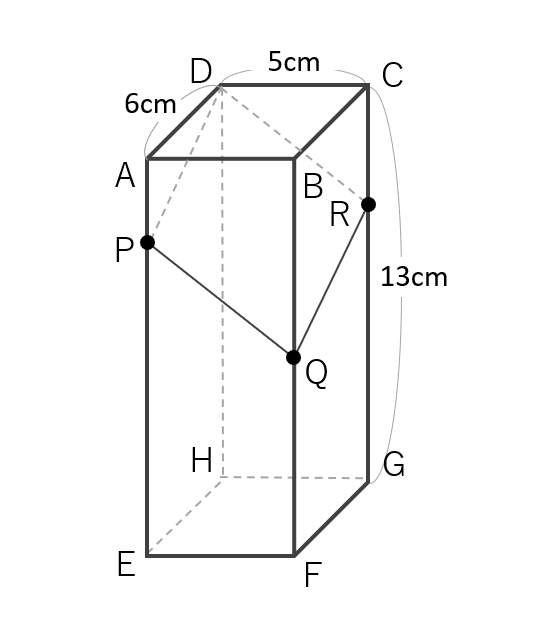
図のような縦６cm，横５cm，高さ13cmの直方体があります。辺AE上にAP＝３cmとなる点Pをとり、辺BF上にBQ＝７cmとなる点Qをとって、３点D，P，Qを通る平面でこの直方体を切り、２つの立体に分けます。次の□に適当な数を入れなさい。
（１）３点D，P，Qを通る平面が辺CGを切る点をRとするとき、四角形QFGRの面積は□㎠です。
（２）切り分けられた２つの立体のうち、大きい方の体積は□㎤です。
慶應義塾中等部（2022年）
名門付属校の慶應義塾中等部より「立体図形（切断）」の問題です。立体切断に関する基本知識が備わっているかを確認することができます。過去問解説記事の使い方を読んだ上で、算数の志望校対策や、得点力アップ、弱点補強にご活用ください。
本問題の難度
Lv.２ 中学受験 標準問題
全受験生にオススメの中学受験算数の標準問題をまとめています。シンプルな問題設定が多いため、算数の各単元のポイント整理にも有効です。本レベルの演習を通じて、受験算数の基礎固めを行いましょう。
※偏差値の目安やその他難度の詳細などはコチラをご覧ください。
解説
（１）四角形QFGRの面積は？
立体図形の切断の問題です。今回は、問題上でどのように切られるかが描かれていますので、ルール通りに必要な部分の長さを図に書き込んでいきましょう。
まずは、問題文に書かれている情報を図に反映しましょう。APは３cm、BQは７cmです。
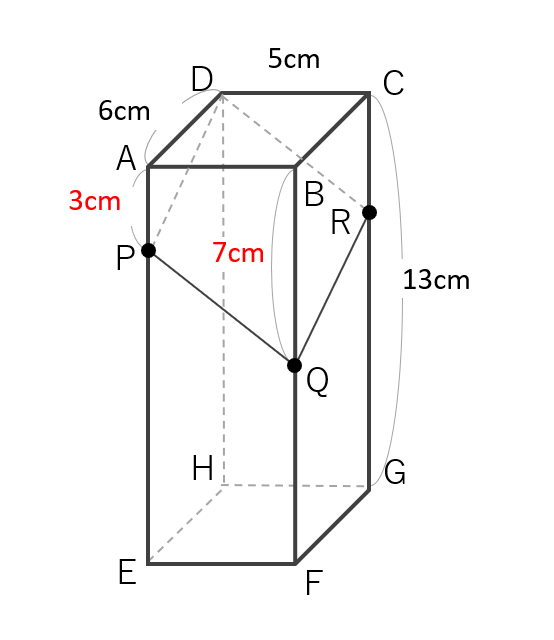
このとき、切り口の一部であるPQはPから右に５cm、下に４cm進む線であることが分かります。
立体切断では、平行な面に出来る切り口の線は必ず平行になるため、PQのある四角形AEFBと平行な面である四角形DHGC上に出来る切り口の線DRは、PQと平行になります。よって、RはCから下に４cmのところにあることが分かります。
プロ家庭教師K四角形BFGCを正面から見ると以下のようになりますね。
あとは台形の面積の公式通りに面積を出しましょう。
よって、四角形QFGRの面積は、（６＋９）×６÷２＝45㎠となります。
プロ家庭教師KRGの長さ９cmは断頭四角柱の性質を利用して、
13＋６＝10＋RG よって、RG＝９cmと求めてもいいですね。
（２）大きい方の立体の体積は？
プロ家庭教師K(２)は、切り分けた後の大きい方の立体の体積です。
今回は四角柱をななめに１回切断した断頭四角柱になるので、高さの平均を使って求めましょう。
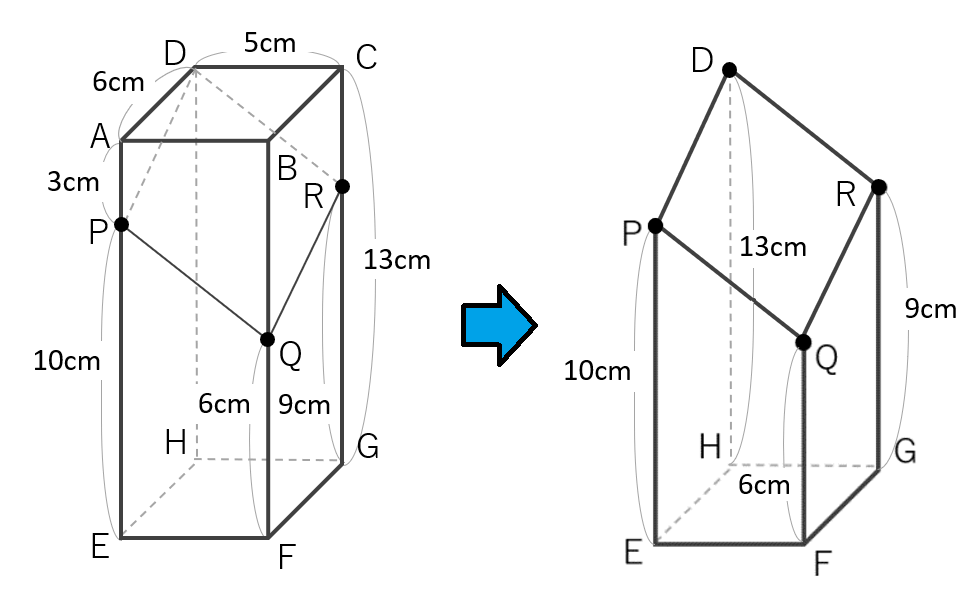
底面積＝６×５＝30㎠
高さ(の平均)＝(13＋６)÷２＝9.5cm
よって、30×9.5＝285㎤が答えとなります。
ピヨまる高さの平均を出す式は、他にもありますね。
・(９＋10)÷２＝9.5cm
・(10＋６＋９＋13)÷４＝9.5cm
プロ家庭教師Kちなみに、先端がとがっているからといって、謎に×\(\large{\frac{１}{３}}\)をしてしまう子がたまにいるよ。すい体ではないので、気を付けよう。
Kとピヨまるの談話室
ピヨまる基本的な立体切断の問題でしたね。
切断時のルールの確認や、断頭四角柱の体積の求め方などの基本ポイントを確認するには良い問題だと思います。
プロ家庭教師Kまとめありがとう。特にいう事なし。
こちらの記事もオススメ☆
・慶應義塾中等部の算数分析／過去問解説はコチラ
・過去問解説記事の一覧はコチラ
・立体図形（切断）の過去問解説はコチラ
・中学受験標準問題（★★☆☆☆）の一覧はコチラ
