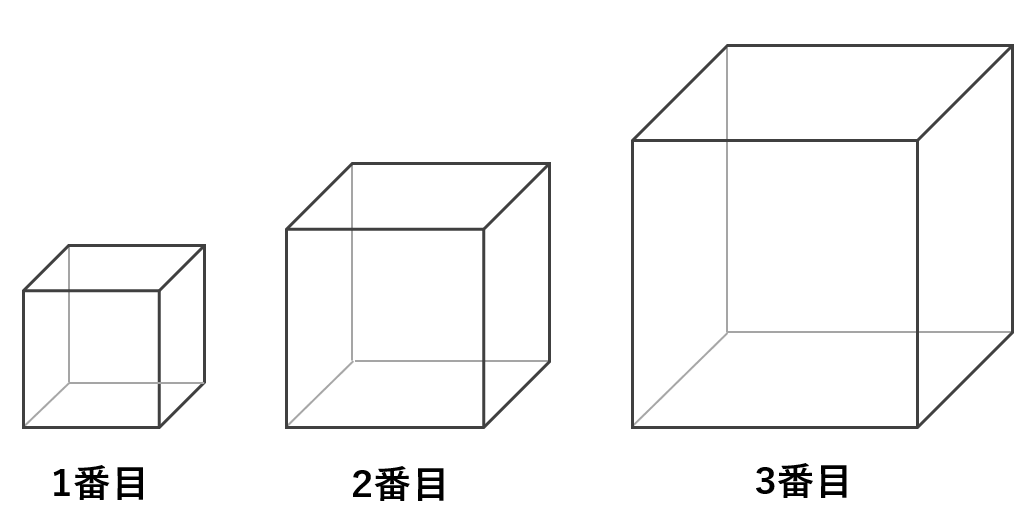
次の□にあてはまる数を答えなさい。
図のように立方体が並んでいて，１番目の立方体の１辺の長さは１cmです。次の立方体の体積が，１つ前の立方体の体積の３倍になるように順に並んでいるとき，16番目の立方体の１辺の長さは□cmです。
三田国際学園中学（2020年）
人気共学校の三田国際学園中学より「立体図形（体積）」の問題です。体積比の理解を深めるのに良い問題です。過去問解説記事の使い方を読んだ上で、算数の志望校対策や、得点力アップ、弱点補強にご活用ください。
本問題の難度
Lv.２ 中学受験 標準問題
全受験生にオススメの中学受験算数の標準問題をまとめています。シンプルな問題設定が多いため、算数の各単元のポイント整理にも有効です。本レベルの演習を通じて、受験算数の基礎固めを行いましょう。
※偏差値の目安やその他難度の詳細などはコチラをご覧ください。
解説
体積比に着目しよう！
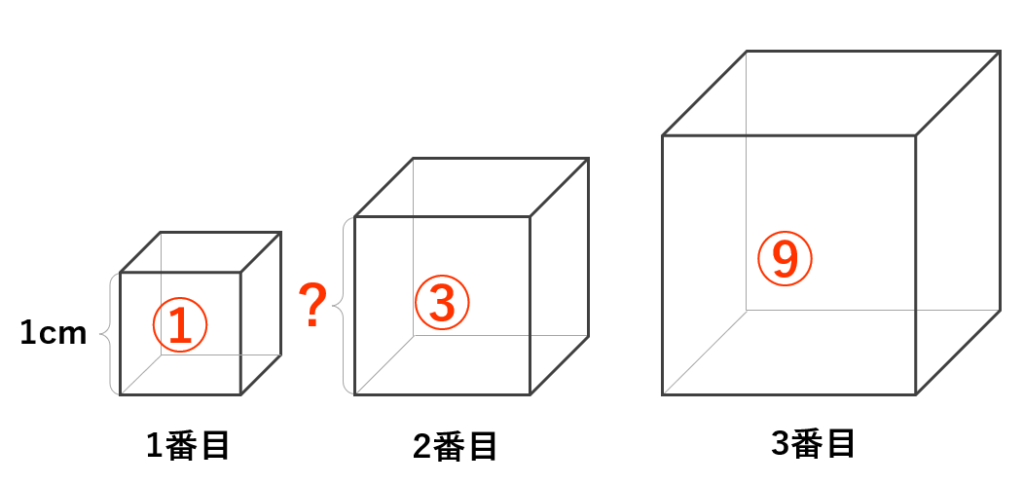
「次の立方体の体積が、１つ前の立方体の体積の３倍になるように順に並べる」と書かれているので、１番目・２番目・３番目の立方体の体積比は、１：１×３：１×３×３＝１：３：９となります。
プロ家庭教師Kありがちな間違いは、体積が３倍という点から早とちりして、１辺の長さが３倍、つまり、２番目の立方体の１辺の長さは３cm、３番目の立方体の１辺の長さは９cmとやってしまうことだね。
ピヨまる２番目の立方体の１辺の長さをAcmとすると、A×A×A＝３㎤ということですよね。１×１×１＝１、２×２×２＝８なので、Aが１cmと２cmの間ってことは分かるけど、ここからどう絞り込んでいけばいいのか・・ブツブツ。
さて、ピヨまる君がブツブツ言いながら悩んでいるように、「A×A×A＝３のとき、Aを求めなさい」というのは中学受験算数の学習範囲では求めることが出来ません。ということで、２番目の立方体でずっと悩み続けるのではなく、１辺の長さが分かる立方体になるまで順番を進めていきましょう。
- １番目 １×１×１＝１㎤
- ２番目 A×A×A＝３㎤
- ３番目 B×B×B＝９㎤
- ４番目 C×C×C＝27㎤
３番目のB×B×B＝９も２番目と同様にBを求めることが出来ないので、４番目に進むと、C×C×C＝27ですが、C＝３のとき、３×３×３＝27になるので、４番目の立方体の１辺の長さは３cmであることが分かります。
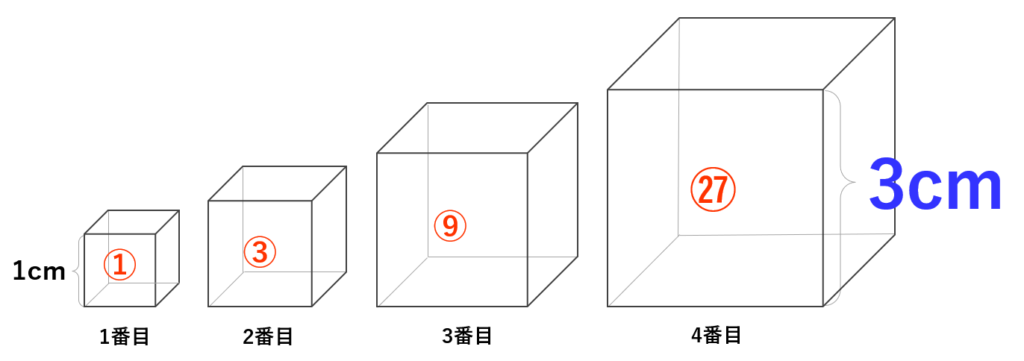
よって、１番目の立方体が１辺の長さが１cmのとき、４番目の立方体の１辺の長さは３倍の３cmとなります。同じように考えると、次は７番目の立方体の１辺の長さはさらに３倍の９cm、10番目の立方体の１辺の長さはさらに３倍の27cm、…と進めていくことが出来るので、16番目の立方体まで進めていきます。
- １番目 １cm
- ４番目 ３cm
- ７番目 ９cm
- 10番目 27cm
- 13番目 81cm
- 16番目 243cm
よって、16番目の立方体の１辺の長さは243cmになります。
Kとピヨまるの談話室
ピヨまる体積比に関連して１つ質問です。
「立方数を覚えておいた方が良い」というネット記事を読んだことがあるんですが、覚えた方がいいですかね？てか、そもそも立方数って何でしたっけ？
プロ家庭教師K立方数は「同じ数を３回掛けた数」ね。例えば、２×２×２＝８、４×４×４＝64の８や64のことを立方数という。
体積比で使うことがあるので「１×１×１～９×９×９まで覚えよ！」という先生もいるけど、個人的にはどちらでもいいと思うよ。まぁ、１，８，27，64，125，216位までは見慣れておいてほしいが。216は場合の数のサイコロの問題でも出てくるね。
覚えたかったら覚えたら？任せるよ。
ピヨまる任されました。う～ん、どうしよっかな～。覚えようかな～。それとも覚えないかな～。ん～、どっちだと思います？
プロ家庭教師K知らん。
こちらの記事もオススメ☆
・三田国際学園中学の算数分析／過去問解説はコチラ
・過去問解説記事の一覧はコチラ
・立体図形（体積と表面積）の過去問解説はコチラ
・中学受験標準問題（★★☆☆☆）の一覧はコチラ
