女子難関校の浦和明の星女子中学の算数分析記事です。今回の過去問分析対象は「2021年入試」になります。浦和明の星女子中学の「算数の傾向と対策」を知り、合格に向けて是非ご活用ください。
【受験生のパパママ】
受験する学校の情報集めや算数分析の一助に!
志望校の傾向を把握すると共に、お子さんの得意分野・苦手分野の洗い出しなど学習サポートにもご活用ください★
【受験生本人】
過去問を解いた後の復習に活用しましょう!
各問題の難易度と自分の〇×を見比べながら、解けた問題は自信に変え、解けなかった問題は徹底復習してください!合格との距離をイメージし、今後どんな勉強をしていけばいいのかを考え、実行しよう★
浦和明の星女子中学 2021年入試結果
配点・試験時間
- 国語 100点(50分)
- 算数 100点(50分)
- 理科/社会 各50点(併せて50分)
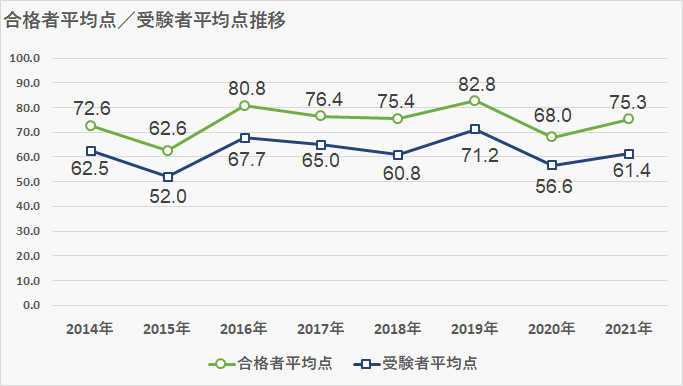
合格者平均点・受験者平均点
- 合格者平均点:75.3点
- 受験者平均点:61.4点
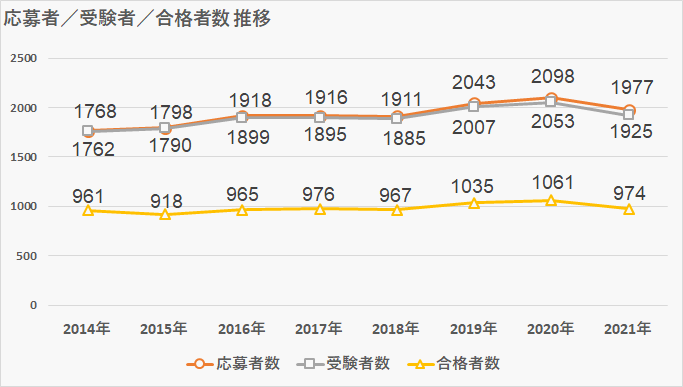
受験者数/合格者数
- 応募者数:1,977人
- 受験者数:1,925人
- 合格者数:974人
- 募集者数:120人
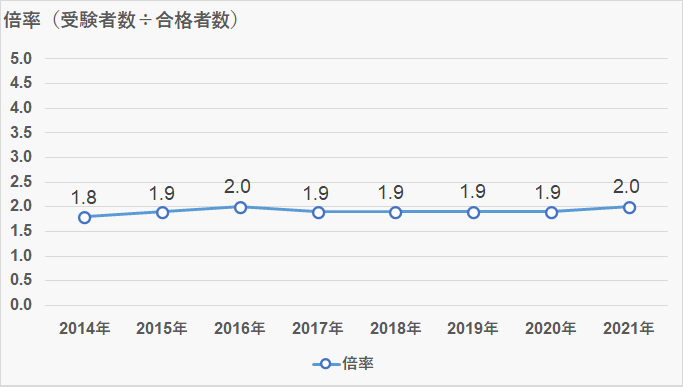
実質倍率
- 倍率:2.0倍
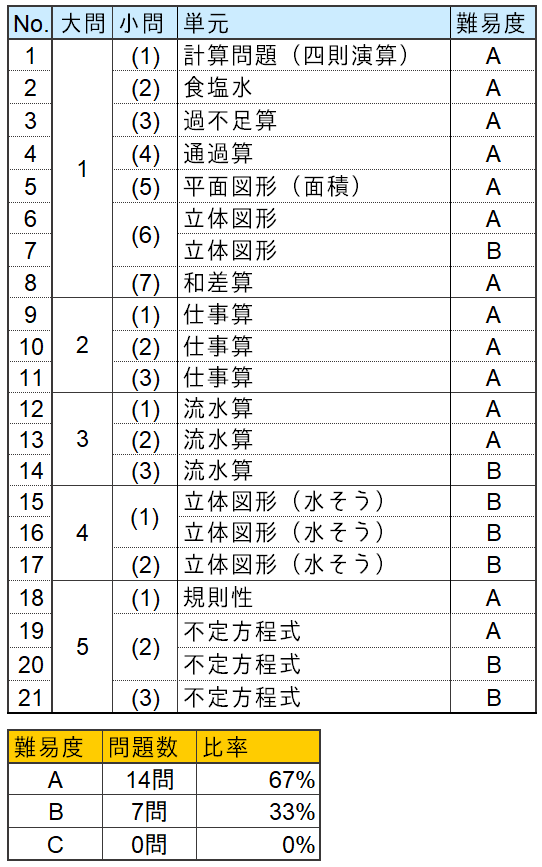
問題別難易度分析
【難易度説明】
A:浦和明の星女子中学合格のために正答したい問題
B:合否を分ける差がつく問題
C:発展問題(間違えても差がつかない)
問題別攻略のポイント
大問1(1) 計算問題(四則演算)
問題数:1
難易度:A
標準的な計算問題です。3.52-2.78=0.74のみ小数で計算し、あとは分数で計算を進めましょう。約分すべきところを最後まで約分出来ていたか等を確認しておきましょう。
大問1(2) 食塩水
問題数:1
難易度:A
基本的な食塩水の問題です。食塩は濃度100%,水は濃度0%の食塩水として考え、ビーカー図で解き進めましょう。
大問1(3) 過不足算
問題数:1
難易度:A
人数が予定と実際で異なっておりますが、元々の人数を①や〇人、実際の人数を③や〇×3人などとして、お菓子の個数を式に表しましょう。過不足算は簡単に検算が出来るので、正答を確認してから次の問題に進むのもオススメです。
大問1(4) 通過算
問題数:1
難易度:A
速さの異なる通過算です。どの程度速さが異なっているのか割合が分かっていますので、速さをそろえて、トンネルに入り始めてから出終わるまでに掛かる時間を40秒から60秒に直して考えましょう。
本問題は当ブログに解説を掲載していますので、よろしければご覧ください。

大問1(5) 平面図形(面積)
問題数:1
難易度:A
半径は分からんが半径×半径は分かる問題です。頻出ポイントですね。大きな半円から白い部分(葉っぱ型の半分)を2つ除いて、斜線部分の面積を出しましょう。なお、直径:半径は2:1なので、直径×直径と半径×半径の面積比は4:1になります。セットで押さえておきましょう。
大問1(6) 立体図形
問題数:2
難易度:A,B
サイコロの絵が描いてあるので、図1のサイコロ&問題文から得られる情報を使いながら、図2のサイコロの絵に目の数を入れていきます。「同じ目の数の面どうしをはりあわせて、…」など問題文の条件を正しく読み解け、使用できたか確認しておきましょう。
左上手前のサイコロが図1と同じ形なので、右の面の目は3(つまり、右上手前のサイコロの左面の目も3)となっている所から1つずつ目を考えていきます。
大問1(7) 和差算
問題数:1
難易度:A
3つの整数の内、1番大きい整数が奇数になっているので、小さい方からア,イ,奇などで表し、解きます。問題文の情報をア+イ+奇=31と奇-イ+奇-ア+イーア=18というように式に直し、考えてみましょう。
奇-イ+奇-ア+イーアは、-イと+イは相殺されるので、奇×2-ア×2が残り、奇×2-ア×2=18となります。これは(奇-ア)×2=18に変換できるので、奇-ア=9。あとは、ア+イ+奇=31に当てはまるように奇とアの候補を1つずつ絞り込んでいきます。
大問2 仕事算
問題数:3
難易度:A,A,A
仕事算の基本問題です。
まずは「1日あたりの仕事量」「全体の仕事量」といった基本情報を出しましょう。式を作ると、Aさん4日分の仕事量=Bさん3日分の仕事量となることが分かるため、Aさん・Bさんの1日あたりの仕事量は3:4、全体の仕事量は、3×12+4×9=72となります。
(3)は、「Aさんが6日休んだ→その間、Bさん・Cさんが2人で働いた」なので、(4+2)×6=36の仕事量を、全体の仕事量から除いて考えましょう。
合格のためには3つとも正答したい問題です。

大問3 流水算
問題数:3
難易度:A,A,B
(1)は、問題文より船Aの上りの速さ=船Bの下りの速さと分かるので、そこから攻めます。船Aの静水時の速さをA、船Bの静水時の速さをBとすると、船Aの上りの速さ=船Bの下りの速さは、A-36=B+36に変換できます。ここまで来れば、AとBが分速72m差であることが分かるでしょう。
(2)は、船Aがイ町に着いた時、1728mの差がついているので、そこから攻めます。船Aの上りと船Bの上りの速さの差は(1)と同様に分速72mであり、1分で2つの船は72mの差が広がります。すると、1728÷72=24、40-24=16より、船Aは上りに24分かかり、下りに16分掛かる事が分かります。(1)から誘導されていますので、小問のつながりを意識して、解き進めましょう。
上りと下りの距離は同じなので、上りに掛かった時間と下りに掛かった時間の比と、速さの比は逆比になり、速さの比は2:3。速さの差は36+36=分速72mとなりますので、ここから答えを出します。
(3)は、問題に描かれたダイヤグラムを使って解きます。ダイヤグラムを平面図形として捉え、相似を使って解くのは頻出パターンですので、押さえておきましょう。
大問4 立体図形(水そう)
問題数:2
難易度:B,B,B
容器Aと容器Bの水の深さを⑥、④として、水の移しが1回1回終わる毎にそれぞれの容器の水の深さを表し、比べてみましょう。
最初に容器Aから容器Bに水を移すと、容器Aの水の深さは⑤、容器Bの水の深さは⑤-0.8となります。さらに容器Aから容器Bに水を移すと、容器Aの水の深さは④、容器Bの水の深さは④+2.4となります。
ここから、容器Aの高さ②分の水量が、容器Bの高さ2.4cm分の水量と同じであることが分かり、解き進めると①が2(cm)であると求められます。
(2)は、容器Aの底面積をもとに容器Bの底面積を求めた後、実際に水の体積を出して計算を進めれば特に問題ないでしょう。(1)が出来れば、取りたい問題です。
大問5 規則性,不定方程式
問題数:4
難易度:A,A,B,B
(1)は、10cmのテープのみをつないで長いテープを作るので、テープの長さは2+8×〇の形で表すことができます。1個目の2+8×6=50cmが見つかった後は、8と10の最小公倍数である40ずつ足していき、当てはまるものが答えとなります。
(2)(3)は、不定方程式です。
3種類のテープを何枚か使って、130cmの長いテープを作るので、2+8×〇+18×□+28×△=130と式化できます。計算できる部分をすると、8×〇+18×□+28×△=128と変換できるので、当てはまるものを探していきます。(使わないテープがあっても良いのかダメなのか必ず確認しましょう。)
(2)は、範囲を出す問題ですので、極端な場面を考えます。テープの枚数を最も多くする場合は1枚あたりが最も短い10cmのテープを多く、テープの枚数を最も少なくする場合は1枚あたりが最も長い28cmのテープを多くという考えのもと、探していきましょう。
(3)に関しては、それぞれのテープを必ず1枚ずつ使うという条件が加わっていますので、それぞれの長さを考慮(128-8-18-28=74cm)して、8×〇+18×□+28×△=74として考えても問題ありません。
Kの考察
2021年度の第1回入試は大問が5つ、問題数は21問。問題レベルは21問中 A問題が14問(67%)、B問題が7問(33%)、C問題が0問(0%)で構成されており、問題形式、数において例年と大差ない年度でした。問題は、設定が複雑な問題や奇問も無く、平易な内容だったと思います。
各種平均点は合格者平均点75.3点、受験者平均 61.4点でした。過去10年間(2011年~2020年)の平均(合格者平均点 74.2点、受験者平均点 62.2点)と比べ、大きな乖離は見られないものの、合格者平均点と受験者平均点の差は13.9点と多少広がる結果となりました。
個別の問題については、大問4(水そう問題)、大問5後半(不定方程式)は、算数が得意な子と苦手な子の差が出やすい分野・差が出やすい難度の問題であったため、合否の分かれ目になったかと思います。
一方で、大問2(仕事算)に関しては、A問題の中でも難度は低いため、素早く正答し、他の問題に時間を掛けられたか等もポイントになったでしょう。
浦和明の星女子中学の算数対策
※現在準備中となります。
浦和明の星女子中学の過去問題集
浦和明の星女子中学関連情報
浦和明の星女子中学の算数分析/過去問解説はコチラ

