ラグビーの試合では、トライを１回決めると５点入ります。トライを決めるとゴールを１回狙うことができ、ゴールを決めるとさらに２点入ります。Nチームは、１試合で123点入りました。Nチームのこの試合でのトライを決めた回数とゴールを決めた回数の組み合わせは、全部で何通りですか。
東京農業大学第一高等学校中等部（2020年）
東京農大第一よりラグビーを題材にした問題です。
過去問解説記事の使い方を読んだ上で、算数の志望校対策や、得点力アップ、弱点補強にご活用ください。
解説
いもづる算の解き方
ラグビーの問題です。算数ですので、ラグビーのルールや得点の仕組みは知らなくても特に問題ありません。まずは、問題文を一読して、得点の取り方はトライ１回５点とトライ＆ゴール１回ずつの７点の２種類であるという点をしっかりと押さえておきましょう。
得点の取り方が２種類あり、合計得点も分かっているので、つるかめ算と判断してしまう子もいるかもしれませんが、今回はトライとトライ＆ゴールの合計の回数が分かっていないので、つるかめ算ではなく、いもづる算（不定方程式）で解きます。
トライを決めた回数を〇回、トライ＆ゴールを決めた回数を▢回とすると、以下のような式を作ることが出来ます。
５点×〇＋７点×□＝123点
プロ家庭教師K〇と□の部分は「xとy」を使って、５×x＋７×y＝123にしても良い。当然、AとBでも良い。普段使っている記号（あるいは文字）を用いよう。
トライを決めた回数とゴールを決めた回数の組み合わせが何通りか？を出すので、〇と□の組み合わせが何通りかを数え出していきます。
中途半端なところからではなく、まず□回のMAX（最大）を考えてみましょう。
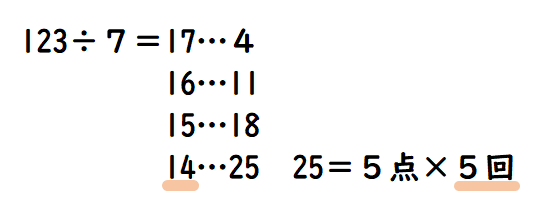
上の画像のように、123÷７＝17…４から始め、７点以外の部分（あまり）が５の倍数になるまで１つずつズラしていきましょう。５の倍数になれば、123点を５点と７点で分けることが出来るという事なので、１個目の組み合わせが見つかります。
１個目の組み合わせは、トライを決めた回数が５回、トライ＆ゴールを決めた回数が14回の時となります。
プロ家庭教師K５×５＋７×14＝123で合計得点123点と一致しますね。
１個目の組み合わせを見つけた後は、最小公倍数を使ってズラしていきます。
５と７の最小公倍数は35ですので、下の画像のように５点は７回増やして、７点は５回減らしてあげると、合計の得点は変わりません。
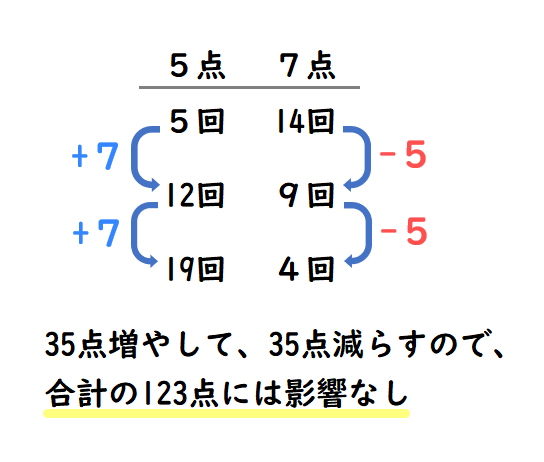
７点のMAXは14回ですので、５回ずつ減らしていくと、□には９回、４回が当てはまりますが、これ以上は減らすことは出来ないので、トライを決めた回数とゴールを決めた回数の組み合わせは３通りとなります。
- 極端な方から１個目を見つける
- １個目を見つけたら、最小公倍数を使ってズラす
プロ家庭教師Kシンプルにトライとゴールに分けて５×〇＋２×□＝123と式を立てても解くことが出来ますね。
ただし、ゴールはトライをしないと出来ないので、トライの回数〇回はゴールの回数□回よりも必ず大きいという条件を忘れないようにしてください。
Kとピヨまるの談話室
ピヨまる2019年はラグビーワールドカップが日本中で盛り上がっていた記憶がありますが、今回の問題は2020年入試ですよね。何か関係があるんでしょうか？
プロ家庭教師K関係はあるだろうね。算数も社会と同様に時事問題がある。例えば、消費税が増税となった翌年の入試では、消費税関連の問題が例年よりも出題されやすいね。でも、大手塾では入試直前に対策をしてくれるはずだから、不安にならなくてもOK。
算数の時事問題が他にどんな問題が出るのか気になる場合は、以下の記事や時事問題がテーマの過去問を参考にしてください。
ピヨまるあざーーーす！
こちらの記事もオススメ☆
・東京農大第一中学の算数分析 / 過去問解説はコチラ
・過去問解説記事の一覧はコチラ
・いもづる算・不定方程式の過去問解説はコチラ
・その他の中学受験標準問題（★★☆☆☆）はコチラ
